1. Motivation
Most portfolio tutorials jump straight into fancy math and end up with something you can’t actually trade. This post goes the other way: we start from the practical pain points investors face and work backward to a solution that stays simple, honest, and robust.
The problem we’re really trying to solve
- Regimes change. Equity booms, commodity spikes, bond selloffs—markets don’t behave the same way month to month.
- Covariances are brittle. Classical mean–variance allocators lean on estimating a huge covariance matrix; small errors there can swing weights wildly.
- Costs and constraints matter. Turnover and position caps aren’t “details”; they decide whether a backtest survives contact with the real world.
- Data is finite. Weekly signals over a decade give you hundreds of decisions, not tens of thousands. Big neural nets overfit easily.
Put simply: a monolithic, end-to-end model that tries to spit out perfect weights every week is hard to trust and easy to overfit.
A calmer approach: switching among strong, simple experts
Instead of learning raw portfolio weights, we build a small set of expert allocators that are already sensible and diversified—specifically HRP (Hierarchical Risk Parity) and HERC (Hierarchical Equal Risk Contribution)—computed over multiple lookback windows. Each expert is a different “lens” on recent market structure. Then we teach a tiny agent to pick one expert (or HOLD the current portfolio) each week.
Why this helps:
- Low dimensional decisions. Choosing among ~a dozen experts is much easier than choosing a 10–50 dimensional weight vector.
- Built-in diversification. HRP/HERC spread risk across clusters without inverting noisy covariance matrices.
- Interpretability. Every weekly action has a human label: “follow HRP-120d,” “follow HERC-252d,” or “HOLD.”
- Graceful failure. If conditions look uncertain, the agent can literally choose to do less (HOLD), reducing churn and mistakes.
What “honest” looks like in this project
We bind the system with the guardrails practitioners actually use:
- No look-ahead. Decisions at time $t$ earn P&L from $t{+}1$.
- Transaction costs are charged on the amount traded.
- Turnover caps limit how fast the portfolio is allowed to change.
- Per-asset caps and optional cash keep allocations sensible and capacity-friendly.
- Weekly cadence keeps the process realistic for most investors and clear enough for readers to follow.
These choices make the backtest slower-moving, but far more believable.
Why Reinforcement Learning fits this problem (and not the other one)
Reinforcement Learning (RL) often gets used to learn weights directly; that’s where you see lots of hype and little reliability. Here we use RL in a narrow, structured role:
- The state is small and meaningful (recent expert performance + a few regime cues).
- The action is discrete (pick an expert or HOLD).
- The reward is exactly what matters to a trader: next-week P&L minus costs and a gentle penalty for excessive turnover, with an optional nudge to HOLD during stress.
This framing lets RL do what it’s good at—sequencing decisions under uncertainty—without asking it to rediscover portfolio theory from scratch.
Why not just pick the “best” expert and stop?
Because “best” changes. Short lookbacks adapt quickly but can whipsaw; long lookbacks are steady but slow. Market clusters evolve. A single expert that dominates in one period can trail badly in another. A meta-controller that learns when to lean on which expert can harvest the strengths of each while sidestepping their worst weeks.
The promise (and the boundaries) of this tutorial
By the end, you’ll have a Colab-friendly pipeline that:
- Downloads ETF data, resamples to weekly, and caches it.
- Precomputes HRP/HERC expert weights across multiple lookbacks.
- Trains a compact PPO agent that chooses among those experts (plus HOLD).
- Evaluates against simple, transparent baselines (Equal Weight, 60/40, Best Single Expert, Random Switcher).
- Reports risk-aware metrics (Sharpe, Sortino, CVaR@5%, Max Drawdown, Turnover, cost drag) with clear plots.
- Enforces realistic constraints (turnover and position caps) so results make sense out of the box.
And we’ll be explicit about what this isn’t: it’s not high-frequency trading, not a data-scraping marathon, and not a black box. It’s a clean, reproducible template you can understand, extend, and stress-test.
A 10-second mental model
Small state → simple action → bounded execution → honest reward. That’s the whole idea.
2. Background
This section gives you just enough background to make the rest of the tutorial feel obvious. We’ll cover (a) why classic mean–variance struggles, (b) what HRP/HERC do in plain English, and (c) how Reinforcement Learning, specifically PPO, fits our switching setup.
2.1 Portfolio allocation in 60 seconds
Classic idea (mean–variance): choose weights $w$ to trade off expected return vs. risk.
- Risk is usually measured by the covariance matrix $\Sigma$.
- A popular formulation: “maximize Sharpe” or “minimize variance for a target return.”
Why it breaks in practice:
- Noisy covariances. Estimating $\Sigma$ from limited data is fragile; tiny errors → big weight swings.
- Leverage to errors. Inverting $\Sigma$ amplifies noise.
- Constraints & costs (turnover limits, position caps, trading fees) are not afterthoughts—they decide whether the backtest survives.
Takeaway: we still care about diversification and risk spreading—but we need methods that are stable under estimation error and honest about trading frictions.
2.2 HRP & HERC (the “robust experts”)
Both HRP (Hierarchical Risk Parity) and HERC (Hierarchical Equal Risk Contribution) try to spread risk without directly inverting a noisy covariance matrix.
HRP in one picture
- Cluster by similarity. Use asset correlations to form a tree (dendrogram): similar assets (e.g., long bonds) group together.
- Order assets by the tree (quasi-diagonalize $\Sigma$) so correlated names sit near each other.
- Top-down allocation. Split capital between clusters by their risk (lower-risk clusters get more), then recurse within each cluster.
Intuition: if two assets move together, you don’t double-count them. You allocate to clusters first, then to members, tempering over-concentration from noisy estimates.
HERC in one picture
HERC follows the same hierarchy, but aims for equal risk contribution at each node in the tree:
- At a parent node, allocate to child clusters so each child contributes equal risk to the parent.
- Recurse down the tree until you reach individual assets.
Intuition: HERC is like “risk parity, but hierarchical.” It embeds risk parity logic inside the cluster tree, yielding smooth, intuitive allocations.
HRP vs HERC (practically)
- HRP: simpler top-down rule-of-thumb risk splits; very stable, cluster-first mindset.
- HERC: more explicit equal-risk balancing along the tree; can be a bit more active about matching contributions.
Why we use both: they’re robust, complementary, and don’t require $\Sigma^{-1}$. With multiple lookbacks (e.g., 60/120/252/… days), each expert sees a different slice of recent history.
2.3 Why “experts across lookbacks”?
Market structure shifts. Short lookbacks react quickly (good in fast trends, bad in chop). Long lookbacks are slow but steady. By computing HRP/HERC across several windows, we get a palette of reasonable portfolios:
Our RL agent won’t try to invent weights from scratch—it will pick which expert to follow this week (or HOLD to keep last week’s weights).
Why this matters: We collapse a hard, high-dimensional problem (“what are the optimal weights?”) into a small, labeled action set (“which expert best fits now?”).
2.4 Reinforcement Learning (RL) for allocation—only the bits we need
An RL problem is a loop:
- State $s_t$: what the agent sees now.
- Action $a_t$: what it decides to do.
- Reward $r_{t+1}$: what it earns after the environment moves.
- Policy $\pi(a|s)$: how it maps states to actions (deterministic or probabilistic).
For us:
- State: compact features—recent performance of each expert + a few regime cues (e.g., a volatility proxy, simple trend flags, a stress indicator).
- Action: choose one expert (or HOLD).
- Reward: next-period net P&L minus transaction costs and a turnover penalty (with an optional bonus to HOLD during stress).
- Transition: decisions are weekly; P&L comes from next week’s returns → no look-ahead.
Why discrete actions? It makes learning stable and interpretable. Every action has a human label: “use HRP-120d,” “use HERC-252d,” or “HOLD.”
2.5 PPO in plain English (why we chose it)
PPO (Proximal Policy Optimization) is a popular policy-gradient method. Think of it as “update the policy, but not too much.”
- It uses a clipped objective: if the new policy strays too far from the old one on a given sample, the update is attenuated.
- It estimates advantages (how much better an action did than expected) using GAE (Generalized Advantage Estimation) for a good bias–variance trade-off.
- It adds a bit of entropy regularization to keep exploration alive (prevents premature collapse to one action).
Why PPO here:
- Stability: the clip and KL safeguards help when rewards are noisy (financial returns are).
- Simplicity: works out-of-the-box with discrete or continuous action spaces.
- Tooling: excellent, well-tested implementations (e.g., Stable-Baselines3) with reproducible training loops.
Why not DQN/SAC/TD3? DQN is for discrete actions but pairs best with value-based targets; SAC/TD3 shine in continuous control but add complexity we don’t need for a small discrete set of actions.
2.6 Costs, turnover, and caps are part of the environment
In many “toy” RL examples, you compute P&L first and subtract costs later. We don’t. We embed:
- Transaction costs: charged on the turnover (how much weights change this step).
- Turnover cap: a hard limit on how far weights can move per decision.
- Per-asset caps and optional cash: prevent extreme bets, improve capacity realism.
This directly shapes behavior: the agent learns that flipping between far-apart experts every week is expensive and often not worth it.
2.7 Metrics primer (how we’ll judge results)
You’ll see these throughout the post:
- Sharpe (annualized): mean return / stdev. Good “overall efficiency” metric.
- Sortino: mean return / downside stdev (penalizes only bad volatility).
- Max Drawdown (MaxDD): worst peak-to-trough loss in the equity curve.
- CVaR@5% (Expected Shortfall): average of the worst 5% returns—tail risk.
- Turnover: average absolute change in weights per step.
- Cost drag: annualized return lost to trading costs.
Why multiple metrics? One number can hide problems. We want efficiency (Sharpe/Sortino), tail safety (CVaR, MaxDD), and tradability (turnover, cost drag).
2.8 Common misconceptions (and our stance)
- “RL will find magical weights.” Not here. RL just chooses among robust experts; it doesn’t replace portfolio theory.
- “Costs are small; ignore them.” At weekly cadence, costs + turnover constraints dominate behavior.
- “Bigger networks are better.” With limited decisions (weekly data), larger nets overfit. We keep it compact and regularized.
- “One expert to rule them all.” Regimes change—hence switching and HOLD.
2.9 What you should remember
- HRP/HERC: tree-based, robust diversification without inverting $\Sigma$.
- Multiple lookbacks: provide diverse, sensible expert options.
- RL framing: small state, discrete actions, honest reward → stable learning.
- PPO: practical, safe updates; great fit for our discrete meta-controller.
- Costs & caps: built into the environment so the agent learns to respect reality.
3. Data & Universe
This section sets up what we trade, how we pull data, and how we turn daily prices into weekly decisions without look-ahead. If you follow this, everything else in the blog “just plugs in.”
3.1 What we trade (simple, diversified ETFs)
We use 10 liquid, broad ETFs that cover equities, rates, credit, gold, and commodities:
Equities (risk-on)
- SPY : US large-cap equities
- IEFA : Developed ex-US equities
- EEM : Emerging markets equities
Treasuries (duration spectrum, risk-off)
- IEI : 3–7y US Treasuries
- IEF : 7–10y US Treasuries
- TLT : 20y+ US Treasuries
Credit (spread risk)
- LQD : Investment-grade corporates
- HYG : High-yield corporates
Diversifiers
- GLD : Gold
- DBC : Broad commodities
Why these? They’re widely traded, have long histories, and give us distinct risk clusters (equity beta, duration, credit spread, real assets). That’s perfect fodder for HRP/HERC.
3.2 Date range & frequency
- History window: as far back as data are reasonable (e.g., 2005-01-01) through your end date (e.g., 2025-09-01).
- Decision cadence: weekly, every Friday (
W-FRI). - Why weekly? Lower churn, clearer cause–effect, and far fewer look-ahead traps (and it’s realistic for many investors).
3.3 Data source & ground rules
- Source:
yfinanceadjusted close (dividends/splits accounted). - Currency: USD (all chosen ETFs are USD).
- Timezone: Use exchange-local timestamps; we’ll resample to weekly Friday close.
- Caching: Save to Parquet for reproducible, quick reloads.
Pitfall: Never compute returns from the raw “Close” when dividends matter; always use Adj Close.
3.4 Daily → weekly (without leakage)
We want:
- A weekly price series (
W-FRI, last price of the week). - A weekly return series: $r_{t} = \frac{P_t}{P_{t-1}} - 1$.
- A decision index
t(Fridays we act on), and a next indext+1(the week after, where P&L is realized).
# Goal: pull daily adjusted closes, resample to weekly (Friday), compute returns,
# and create decision/next-week indices with NO look-ahead.
import pandas as pd, numpy as np, yfinance as yf
from pathlib import Path
TICKERS = ["SPY","IEFA","EEM","IEI","IEF","TLT","LQD","HYG","GLD","DBC"]
START = "2005-01-01"
END = "2025-09-01"
cache_dir = Path("data"); cache_dir.mkdir(exist_ok=True)
# 1) Download daily adjusted closes
daily_px = yf.download(TICKERS, start=START, end=END, auto_adjust=False, progress=False)["Adj Close"]
daily_px = daily_px.sort_index()
# 2) Weekly Friday close (end-of-week snapshot)
weekly_px = daily_px.resample("W-FRI").last()
# 3) Weekly simple returns
weekly_rets = weekly_px.pct_change().dropna(how="all")
# 4) Decision dates and next-week mapping
dates_t = weekly_rets.index[:-1] # we can act on these weeks
dates_tp1 = weekly_rets.index[1:] # P&L realized here
# 5) Save caches
weekly_px.to_parquet(cache_dir / "weekly_prices.parquet")
weekly_rets.to_parquet(cache_dir / "weekly_returns.parquet")
Check: After resampling, every return at time $t+1$ uses only information through $t$. We will always pick an action at $t$ and score P&L using
weekly_rets.loc[t+1].
3.5 Handling missing data & ETF inception
Some ETFs launched later. Early rows will have NaN for those tickers. Options:
- Strict windowing (recommended): when you compute expert weights on a given date, use only assets with a full lookback window of data (drop assets with missing values within the window).
- Forward-fill within week: fine after resampling (no daily leakage), but do not forward-fill across inception gaps.
- Masking: keep the column but set its weight to zero before normalization if data are insufficient.
def window_returns(weekly_rets: pd.DataFrame, end_date, lookback_weeks: int) -> pd.DataFrame:
"""Slice a clean return window ending at end_date (exclusive)."""
end_pos = weekly_rets.index.get_loc(end_date)
start_pos = max(0, end_pos - lookback_weeks)
win = weekly_rets.iloc[start_pos:end_pos]
# Drop columns with any NaN in the window (strict)
win = win.dropna(axis=1, how="any")
return win
Pitfall: Treating “pre-inception” as zeros biases returns. Prefer dropping those assets for that window or masking their weights to 0.
3.6 Transaction costs & turnover
We charge a simple, transparent cost each time we change weights:
- Cost model: $\text{cost}t = c{\text{bps}} \times \text{turnover}_t$
- Turnover: $\text{turnover}t = \sum_i |w{t,i} - w_{t-1,i}|$
- Default: $c_{\text{bps}} = 2$ (i.e., 2 bps per unit turnover per week)
This is built into the reward—the agent feels costs immediately.
Why this model? It’s conservative but realistic for weekly ETF portfolios and easy to reason about. You can stress it to 5–10 bps later.
3.7 Position & turnover caps (guardrails)
We enforce simple constraints that keep the strategy tradable:
- Per-asset cap: $w_{t,i} \le 35%$
- Optional cash: allow up to 5% idle cash if experts under-allocate after caps.
- Turnover cap: $\sum_i |w_{t,i} - w_{t-1,i}| \le 20%$
A small helper ensures weights stay on the simplex and respect caps:
def clip_and_normalize(weights: pd.Series,
max_per_asset: float = 0.35,
min_cash: float = 0.00,
max_cash: float = 0.05) -> pd.Series:
"""Clip per-asset caps, allow small cash band, renormalize to <= 1."""
w = weights.clip(lower=0.0, upper=max_per_asset)
s = w.sum()
if s > 1.0 - min_cash:
w = w / s * (1.0 - min_cash)
# Add cash if sum < 1 - max_cash (rare with caps), else keep within [1-max_cash, 1]
total = w.sum()
cash = max(0.0, min(max_cash, 1.0 - total))
return (w, cash)
def apply_turnover_cap(w_prev: pd.Series, w_raw: pd.Series, cap: float = 0.20) -> pd.Series:
"""Scale the step toward w_raw so that L1 change ≤ cap."""
delta = w_raw - w_prev
l1 = delta.abs().sum()
if l1 <= cap + 1e-12:
return w_raw
scale = cap / l1
return w_prev + scale * delta
Why caps matter: They prevent the agent from ping-ponging between distant experts, keeping turnover and impact under control.
3.8 Building decision/next indices (the leak-proof loop)
We’ll use two aligned indices throughout the code:
# dates_t : when we DECIDE (index 0 .. N-2)
# dates_tp1 : when we REALIZE (index 1 .. N-1)
dates_t = weekly_rets.index[:-1]
dates_tp1 = weekly_rets.index[1:]
# Example (pseudo-code): at time t
for t, tp1 in zip(dates_t, dates_tp1):
# 1) Build features from data available up to t (inclusive)
# 2) Pick action a_t (expert or HOLD)
# 3) Get weights w_t (after caps & turnover cap vs w_{t-1})
# 4) Realize pnl_{t+1} = w_t · weekly_rets.loc[tp1]
# 5) Subtract costs (based on |w_t - w_{t-1}|)
Sanity check:
tp1is always strictly aftert. Nothing fromtp1leaks into the decision att.
3.9 Caching layout (so runs are fast & reproducible)
We’ll keep a predictable folder structure:
data/
weekly_prices.parquet
weekly_returns.parquet
experts_cache/
hrp_lookback_<X>d.parquet
herc_lookback_<Y>d.parquet
models/
ppo_best.zip
outputs/
figures/
csv/
- Why Parquet? Columnar, compressed, preserves dtypes, and loads fast.
3.10 Quick health checks (do these once!)
After loading & resampling:
assert weekly_px.index.is_monotonic_increasing
assert weekly_rets.index.equals(weekly_px.index[1:]) # returns start after first price
assert weekly_rets.isna().all(axis=1).sum() == 0 # no all-NaN rows
assert weekly_rets.abs().max().max() < 1.0 # sanity: weekly returns should be <100%
Visual spot-check (optional):
ax = (1 + weekly_rets["SPY"]).cumprod().plot(title="SPY weekly cumulative (spot-check)")
ax.set_xlabel("Date"); ax.set_ylabel("Cumulative gross");
If something looks off: verify you used Adj Close, and that
W-FRIresampling aligns with your reward timing.
3.11 Parameter summary (you can copy-paste)
universe:
tickers: [SPY, IEFA, EEM, IEI, IEF, TLT, LQD, HYG, GLD, DBC]
dates:
start: 2005-01-01
end: 2025-09-01
frequency: W-FRI
costs:
trade_cost_bps: 2.0 # per unit turnover per decision
constraints:
max_per_asset: 0.35
turnover_cap: 0.20
cash_allowed: true
max_cash: 0.05
resampling:
price: Adj Close
rule: W-FRI
3.12 What to remember
- Use Adj Close, resample to W-FRI, compute returns cleanly, and separate decision/realization indices.
- Embrace missing-data discipline around ETF inceptions (drop or mask, don’t invent returns).
- Bake costs and caps into the environment so the agent learns behavior you can actually trade.
4. Expert Allocators
This is where we build the experts our RL policy will choose from: HRP and HERC, each computed over multiple lookback windows. We’ll (a) define the experts, (b) compute their weights for every decision date, (c) apply caps & normalization, and (d) cache everything so training runs are fast and reproducible.
4.1 What counts as an “expert” here?
An expert is a fully specified portfolio rule that maps a window of past returns to a weight vector $w$ over our ETF universe. We use:
- HRP (Hierarchical Risk Parity)
- HERC (Hierarchical Equal Risk Contribution)
…and we compute each of them on several lookbacks (e.g., 60, 120, 252, 504, 756, 1008 trading days). That gives us 12 experts total:
Why daily lookbacks if we make weekly decisions? Because covariance and clustering are more stable on daily returns. We still resample to weekly for decisions and rewards; we just let the experts “see” richer daily history before each Friday decision.
4.2 Inputs and discipline (no look-ahead)
At each decision Friday $t$:
- Take the daily return window ending at or before $t$.
- Compute HRP/HERC on that window → get raw weights $w^{\text{raw}}_t$.
- Apply per-asset caps and normalization (no shorting).
- Store the capped-normalized weights $w_t$ for this expert at date $t$.
- Later, when we evaluate performance, we’ll multiply $w_t$ by next week’s returns $r_{t+1}$.
We never peek into $t{+}1$ to make the decision at $t$.
4.3 Implementation sketch (with safe defaults)
Below is a practical template. It assumes you already built:
daily_px(Adj Close, daily) andweekly_rets(weekly, from Section 3)TICKERS(list of 10 ETFs)- Caps:
max_per_asset=0.35, optional cash ≤0.05
You can use
riskfolio-libfor HRP/HERC. If you prefer not to depend on it, swap in your own HRP/HERC implementations or fall back to inverse-variance as a safety net.
# Goal: For every decision Friday t and every lookback window,
# compute expert weights (HRP/HERC), cap & normalize, and cache.
import pandas as pd, numpy as np
from pathlib import Path
from typing import Dict, Tuple
# --- Helpers from Section 3 (lightly adapted) ------------------------------
def clip_and_normalize_long_only(w: pd.Series, max_per_asset=0.35, max_cash=0.05) -> pd.Series:
"""Long-only caps with small optional cash; renormalize to <= 1."""
w = w.reindex(TICKERS).fillna(0.0).clip(lower=0.0, upper=max_per_asset)
s = w.sum()
if s > 1.0:
w = w / s # avoid >1 after capping
s = 1.0
cash = min(max_cash, max(0.0, 1.0 - s))
w["CASH"] = cash
return w
def get_daily_returns_window(daily_px: pd.DataFrame, end_date, lookback_days: int) -> pd.DataFrame:
"""Slice daily returns ending on or before end_date (exclusive of end_date+1)."""
daily_rets = daily_px.pct_change().dropna(how="all")
# Find last daily index <= end_date
end_loc = daily_rets.index.searchsorted(pd.Timestamp(end_date), side="right")
start_loc = max(0, end_loc - lookback_days)
win = daily_rets.iloc[start_loc:end_loc]
# Drop assets with any NaN in the window to avoid contaminating covariances
win = win.dropna(axis=1, how="any")
return win
# --- HRP/HERC wrappers (riskfolio-lib), with safe fallbacks -----------------
def hrp_weights(returns_win: pd.DataFrame) -> pd.Series:
"""Compute HRP weights; fallback to inverse-variance if needed."""
try:
import riskfolio as rp
port = rp.HCPortfolio(returns=returns_win)
w = port.optimization(model='HRP',
codependence='pearson', # correlation
covariance='ledoit', # robust cov
objective='MinRisk', # or 'Utility'
max_k=10, linkage='ward')
w = w.iloc[:, 0] # first (and only) column as Series
return w.reindex(returns_win.columns).fillna(0.0)
except Exception:
# Fallback: inverse-variance portfolio (no clustering)
var = returns_win.var().replace(0.0, np.nan)
ivp = (1.0 / var)
ivp = ivp / ivp.sum()
return ivp.fillna(0.0)
def herc_weights(returns_win: pd.DataFrame) -> pd.Series:
"""Compute HERC weights; fallback to HRP or IVP."""
try:
import riskfolio as rp
port = rp.HCPortfolio(returns=returns_win)
w = port.optimization(model='HERC',
codependence='pearson',
covariance='ledoit',
objective='MinRisk',
max_k=10, linkage='ward')
w = w.iloc[:, 0]
return w.reindex(returns_win.columns).fillna(0.0)
except Exception:
# If HERC fails, try HRP; then IVP
try:
return hrp_weights(returns_win)
except Exception:
var = returns_win.var().replace(0.0, np.nan)
ivp = (1.0 / var); ivp = ivp / ivp.sum()
return ivp.fillna(0.0)
# --- Expert cache builder ---------------------------------------------------
def build_expert_cache(daily_px: pd.DataFrame,
weekly_rets: pd.DataFrame,
lookbacks_days=(60,120,252,504,756,1008),
out_dir="experts_cache") -> Dict[str, Path]:
"""
For each expert and decision date, store capped-normalized weights.
Returns a dict mapping expert_name -> parquet path.
"""
out = Path(out_dir); out.mkdir(exist_ok=True)
dates_t = weekly_rets.index[:-1] # decision dates
registry: Dict[str, Path] = {}
for model in ("HRP", "HERC"):
for L in lookbacks_days:
expert_name = f"{model.lower()}_{L}d"
rows = []
for t in dates_t:
win = get_daily_returns_window(daily_px, end_date=t, lookback_days=L)
# Ensure we only consider assets present in this window
present = [c for c in TICKERS if c in win.columns]
if len(present) < 2:
# Too few assets → default to zero weights (all cash handled by cap/normalize)
w_raw = pd.Series(0.0, index=TICKERS)
else:
if model == "HRP":
w_raw = hrp_weights(win[present])
else:
w_raw = herc_weights(win[present])
w_raw = w_raw.reindex(TICKERS).fillna(0.0)
w_capped = clip_and_normalize_long_only(w_raw)
w_capped.name = t
rows.append(w_capped)
weights_df = pd.DataFrame(rows, index=dates_t)
path = out / f"{expert_name}.parquet"
weights_df.to_parquet(path)
registry[expert_name] = path
return registry
What this does:
- Builds one Parquet per expert, where each row = decision date $t$, columns = ETFs +
CASH. - Each row is long-only, respects the per-asset cap, and includes tiny optional cash if the expert under-allocates after capping.
- No turnover cap here—that belongs to the execution step (the RL environment will enforce it between $w_{t-1}$ and $w_t$).
4.4 Sanity checks (you want these!)
Run these after building one or two experts:
# Load a sample expert to inspect
sample = pd.read_parquet("experts_cache/hrp_252d.parquet")
assert (sample[TICKERS] >= -1e-12).all().all() # no shorts
assert (sample[TICKERS] <= 0.35 + 1e-12).all().all() # per-asset cap holds
row_sums = sample[TICKERS].sum(axis=1) + sample["CASH"]
assert (row_sums <= 1.0000001).all() # never exceed 100%
print("Sample rows:\n", sample.head(3))
Visual gut-check (optional):
(sample[TICKERS].sum(axis=1)).plot(title="HRP-252d: Invested fraction (ex-cash)")
Tip: Investigate dates where invested fraction dips—those often coincide with many caps binding or few assets meeting the lookback window requirement.
4.5 Turning expert weights into “next-week performance labels”
The RL state uses recent performance of each expert as features. To compute that, we need each expert’s realized next-week return for every decision date:
def realized_next_week_perf(expert_weights: pd.DataFrame, weekly_rets: pd.DataFrame) -> pd.Series:
"""
Given one expert's weights over dates t, compute its next-week return r_{t+1}.
Assumes expert_weights index aligns with weekly_rets.index[:-1].
"""
dates_t = expert_weights.index
dates_tp1 = weekly_rets.index[1:]
# Align shapes: drop last return row to match t -> t+1 mapping
R_tp1 = weekly_rets.loc[dates_tp1, TICKERS]
W_t = expert_weights.loc[dates_t, TICKERS]
# Matrix multiply row-wise: (W_t * R_{t+1}).sum over columns
perf_tp1 = (W_t.values * R_tp1.values).sum(axis=1)
return pd.Series(perf_tp1, index=dates_t, name="next_week_return")
We’ll store these per-expert “labels” (next-week returns) to build compact state features like “sum of the last 4 weeks of next-week-returns,” etc.
Why not include costs here? These are expert labels used as state inputs, not executed trades. Costs are charged on the policy’s weight changes (Section 6).
4.6 Design choices you can tweak (and how they trade off)
-
Lookbacks:
- Short (60–120d): faster to adapt, more whipsaw.
- Long (504–1008d): steadier, slower to react.
- Mix: gives the policy diverse options; more experts = richer state but higher compute.
-
Covariance & codependence:
codependence='pearson'andcovariance='ledoit'are robust defaults.- You can try Kendall or Spearman correlations when tails/outliers bother you.
-
Objective:
objective='MinRisk'yields conservative weights;- for more aggressiveness, use a utility or Sharpe-like objective if supported in your HRP/HERC implementation.
-
Fallback policy:
- Keep inverse-variance (IVP) as a final safety net—better a sensible fallback than a crash.
4.7 What not to do (common pitfalls)
- Don’t forward-fill pre-inception data; drop that asset for that window or give it zero weight.
- Don’t bake turnover caps into the expert calculation; enforce turnover when switching between last week’s portfolio and the chosen expert’s weights.
- Don’t allow silent short weights; stay long-only unless your entire pipeline (costs, borrow) handles shorts.
4.8 Outputs & registry (so the RL loop can find experts fast)
Create a tiny registry mapping expert names to their Parquet paths:
registry = build_expert_cache(daily_px, weekly_rets)
# Example:
# {
# 'hrp_60d': Path('experts_cache/hrp_60d.parquet'),
# 'herc_60d': Path('experts_cache/herc_60d.parquet'),
# ...
# }
Later, in the environment, you’ll load each expert’s weight frame once and index rows by decision date $t$. This keeps the RL step() function O(1) for weight lookup.
5. The RL Framing
We’ll now turn the pieces from Sections 3–4 into a small, leak-proof Gym-style environment the PPO agent can learn from. The recipe is: compact state → discrete action → bounded execution → honest reward.
5.1 Overview (what happens each week)
At each decision Friday $t$:
-
Build the state $s_t$ from information available up to and including $t$.
-
Choose an action $a_t$ from a small, discrete set: 12 experts (HRP/HERC × lookbacks) + HOLD.
-
Execute by mapping the action to target weights $w^{\star}t$, then enforcing per-asset caps and a turnover cap against last week’s weights $w{t-1}$ to get final weights $w_t$.
-
Realize reward one week later using next week’s returns $r_{t+1}$:
$$ r_{t+1} = w_t^\top r_{t+1} - c_{\text{bps}}\cdot \text{turnover}_t - \kappa \cdot \text{turnover}t + b{\text{hold}}\cdot\mathbf{1}{\text{stress}_t \land a_t=\text{HOLD}}. $$
-
Advance to $t{+}1$ and repeat.
No data from $t{+}1$ influences the decision at $t$.
5.2 Action space (simple & human-readable)
Let there be 12 expert actions plus 1 HOLD:
A = {
0: hrp_60d, 1: hrp_120d, 2: hrp_252d, 3: hrp_504d, 4: hrp_756d, 5: hrp_1008d,
6: herc_60d, 7: herc_120d, 8: herc_252d, 9: herc_504d, 10: herc_756d, 11: herc_1008d,
12: HOLD
}
- Expert action: copy that expert’s capped weights for date $t$ as your target $w^{\star}_t$.
- HOLD: set $w^{\star}t = w{t-1}$ (keep last week’s portfolio).
Why discrete? It’s interpretable (“this week we followed HERC-252d”) and stable for PPO.
5.3 State (compact, informative, leak-proof)
We keep the state small but meaningful:
5.3.1 Expert performance features (36 dims)
For each expert $e \in {1,\dots,12}$, precompute its realized next-week performance series ${\pi^e_\tau}$ (Section 4.5). At time $t$, build rolling sums over the past 1, 4, and 12 weeks (i.e., windows ending at $t$):
$$ x^{(e,1)}t = \sum{k=1}^{1} \pi^e_{t-k},\quad x^{(e,4)}t = \sum{k=1}^{4} \pi^e_{t-k},\quad x^{(e,12)}t = \sum{k=1}^{12} \pi^e_{t-k}. $$
Concatenate across all experts: $12 \times 3 = 36$ features.
Why: These encode who has been working recently at multiple horizons without peeking into $t{+}1$.
5.3.2 Regime features (4 dims)
-
EWMA volatility proxy (e.g., 20-day daily EWMA of SPY, sampled at $t$, rescaled to weekly).
-
Trend flags: $\text{sign}(\text{SMA}{50} - \text{SMA}{200})$ for SPY and TLT (−1/0/+1).
-
Stress flag: binary $\mathbf{1}{\text{stress}_t}$ where, for example,
$$ \text{stress}t = \big(r^{\text{SPY}}{t} < -1%\big)\ \land\ \big(r^{\text{IEF}}_{t} > +0.3%\big). $$
(Both are weekly returns at $t$.)
Total: 40 dimensions.
Keep scaling simple: standardize/clip each feature to reasonable ranges (e.g., winsorize at 1st/99th percentile) to stabilize learning.
Sketch to build features at time $t$:
def build_state(t, expert_perf: dict, weekly_rets, daily_px) -> np.ndarray:
# expert_perf: name -> pd.Series of realized next-week returns indexed by decision dates
feats = []
for name in EXPERT_NAMES:
s = expert_perf[name].loc[:t].iloc[:-0] # up to t-1 inclusive
feats += [s.tail(1).sum(), s.tail(4).sum(), s.tail(12).sum()]
# regime
spy = daily_px["SPY"]; t_daily = spy.index.searchsorted(t, side="right")
ewma20 = spy.pct_change().ewm(span=20).std().iloc[:t_daily].iloc[-1]
# weekly trends at t
spy_w = weekly_rets["SPY"].loc[:t].iloc[:-0]
tlt_w = weekly_rets["TLT"].loc[:t].iloc[:-0]
spy_ma50 = spy.rolling(50).mean().iloc[:t_daily].iloc[-1]
spy_ma200= spy.rolling(200).mean().iloc[:t_daily].iloc[-1]
tlt_ma50 = daily_px["TLT"].rolling(50).mean().iloc[:t_daily].iloc[-1]
tlt_ma200= daily_px["TLT"].rolling(200).mean().iloc[:t_daily].iloc[-1]
trend_spy = np.sign(spy_ma50 - spy_ma200)
trend_tlt = np.sign(tlt_ma50 - tlt_ma200)
stress = int((weekly_rets["SPY"].loc[t] < -0.01) and (weekly_rets["IEF"].loc[t] > 0.003))
feats += [float(ewma20), float(trend_spy), float(trend_tlt), float(stress)]
return np.asarray(feats, dtype=np.float32)
(Pseudocode; align indices carefully in your implementation.)
5.4 Execution & turnover cap (how actions become tradable weights)
-
Let $w_{t-1}$ be the portfolio you actually held last week.
-
From the chosen action:
- If HOLD: $w^{\star}t = w{t-1}$.
- Else Expert $e$: load that expert’s capped weights for date $t$ as $w^{\star}_t$.
-
Apply turnover cap (e.g., 20% L1): scale the step toward $w^{\star}_t$ so that $|w^{\star}t - w{t-1}|_1 \le 0.20$. This yields executed $w_t$.
-
Transaction cost is charged on the executed turnover: $\text{turnover}t = |w_t - w{t-1}|_1$.
This keeps the agent from ping-ponging between distant experts. It also makes HOLD genuinely valuable in choppy regimes.
5.5 Reward (what the agent actually learns from)
We directly optimize net outcomes:
- PnL: $w_t^\top r_{t+1}$ (portfolio return next week).
- Trading cost: $c_{\text{bps}} \cdot \text{turnover}t$ (e.g., $c{\text{bps}}=2$).
- Turnover penalty: $\kappa \cdot \text{turnover}_t$ (shapes behavior even when costs are low).
- HOLD bonus in stress: a small $b_{\text{hold}}>0$ only when $\text{stress}_t$ and action is HOLD.
Optional: add a gentle drawdown penalty (Section 6 expands) if you want the agent to explicitly prefer smooth equity curves.
5.6 Environment skeleton (Gymnasium-style)
Below is a minimal, readable skeleton you can adapt. It assumes you’ve already built:
experts_weights[name]: DataFrame of weights per decision date $t$ (from Section 4).expert_perf[name]: Series of realized next-week returns for features.weekly_rets: DataFrame of weekly returns (Section 3).- Helper functions:
apply_turnover_cap,clip_and_normalize(already shown earlier).
import gymnasium as gym
import numpy as np
import pandas as pd
class MetaAllocatorEnv(gym.Env):
"""
Discrete meta-controller over precomputed experts + HOLD.
Observation: 40-dim vector (36 expert-perf features + 4 regime cues).
Action: 0..11 = experts, 12 = HOLD.
Reward: next-week net P&L - costs - turnover penalty + optional HOLD bonus in stress.
"""
def __init__(self,
weekly_rets: pd.DataFrame,
experts_weights: dict, # name -> DataFrame (rows: dates t; cols: tickers + CASH)
expert_perf: dict, # name -> Series of next-week returns labeled by t
tickers: list,
trade_cost_bps: float = 2.0,
kappa_turnover: float = 0.002,
hold_bonus: float = 0.0005,
turnover_cap: float = 0.20):
super().__init__()
self.tickers = tickers
self.R = weekly_rets
self.experts_weights = experts_weights
self.expert_perf = expert_perf
# Indices: decisions at t, realization at t+1
self.dates_t = self.R.index[:-1]
self.dates_tp1 = self.R.index[1:]
self._T = len(self.dates_t)
# Costs/penalties
self.c_bps = trade_cost_bps / 10000.0
self.kappa = kappa_turnover
self.b_hold = hold_bonus
self.cap = turnover_cap
# Action/observation spaces
self.action_space = gym.spaces.Discrete(13)
self.observation_space = gym.spaces.Box(
low=-np.inf, high=np.inf, shape=(40,), dtype=np.float32
)
# Internal state
self._i = None
self._w_prev = None # last executed weights (Series over tickers + CASH)
# --- feature builder (align carefully in your code) ---
def _build_obs(self, t) -> np.ndarray:
feats = []
for name in EXPERT_NAMES: # fixed order matching action mapping
s = self.expert_perf[name].loc[:t]
feats += [s.tail(1).sum(), s.tail(4).sum(), s.tail(12).sum()]
# simple regime cues
spy_r = self.R["SPY"].loc[t]
ief_r = self.R["IEF"].loc[t]
stress = 1.0 if (spy_r < -0.01 and ief_r > 0.003) else 0.0
# quick trend proxies (replace with robust daily-based SMAs if you cache them)
feats += [float(self.R["SPY"].loc[:t].rolling(12).std().iloc[-1]), # coarse vol proxy
float(np.sign(self.R["SPY"].loc[:t].rolling(10).mean().iloc[-1])),
float(np.sign(self.R["TLT"].loc[:t].rolling(10).mean().iloc[-1])),
stress]
return np.asarray(feats, dtype=np.float32)
def reset(self, *, seed=None, options=None):
super().reset(seed=seed)
self._i = 0
t0 = self.dates_t[self._i]
# start from equal weight (ex-cash), or load a warm-start portfolio
w0 = pd.Series(1.0/len(self.tickers), index=self.tickers)
w0["CASH"] = 0.0
self._w_prev = w0
obs = self._build_obs(t0)
info = {"date": t0}
return obs, info
def step(self, action: int):
t = self.dates_t[self._i]
tp1 = self.dates_tp1[self._i]
# Map action -> target weights
if action == 12: # HOLD
w_target = self._w_prev.copy()
else:
name = ACTION_TO_EXPERT[action]
w_target = self.experts_weights[name].loc[t].copy()
# Enforce turnover cap vs last executed
w_exec = apply_turnover_cap(self._w_prev[self.tickers], w_target[self.tickers], cap=self.cap)
w_exec = w_exec.reindex(self.tickers).fillna(0.0)
# Re-attach cash (keep target cash or recompute small band)
cash = 1.0 - float(w_exec.sum())
w_exec = pd.concat([w_exec, pd.Series({"CASH": max(0.0, cash)})])
# Compute reward components
pnl = float((w_exec[self.tickers].values * self.R.loc[tp1, self.tickers].values).sum())
turnover = float(np.abs(w_exec[self.tickers] - self._w_prev[self.tickers]).sum())
cost = self.c_bps * turnover
stress = (self.R.loc[t, "SPY"] < -0.01) and (self.R.loc[t, "IEF"] > 0.003)
hold_bonus = self.b_hold if (stress and action == 12) else 0.0
reward = pnl - cost - self.kappa * turnover + hold_bonus
# Advance
self._w_prev = w_exec
self._i += 1
done = self._i >= self._T
if not done:
obs = self._build_obs(self.dates_t[self._i])
info = {"date": self.dates_t[self._i], "turnover": turnover}
else:
obs, info = None, {"done": True}
return obs, float(reward), done, False, info
Notes:
- In real code, compute the trend and vol features from daily caches for stability (Section 3).
- Feature scaling (e.g., standardization/winsorization) can improve PPO stability.
- Keep action→expert mapping fixed and documented.
5.7 Leakage & alignment checks (put these in tests)
- Indexing: assert that for every step,
tp1is strictly aftert. - State purity: your
_build_obs(t)must never use any data fromtp1or later. - Weights sanity: non-negative, per-asset cap respected, sum ≤ 1 (cash soaks the rest).
- Turnover math:
turnover = L1(w_t - w_{t-1})andcost = c_bps * turnover.
assert all(tp1 > t for t, tp1 in zip(env.dates_t, env.dates_tp1))
5.8 Practical PPO tips (for this environment)
- Discrete policy (Categorical) with a small MLP (e.g., 2 layers: 1024 → 512) is plenty at weekly cadence.
- Entropy: keep a small entropy bonus to avoid collapsing prematurely onto one expert.
- Advantage norm & reward scale: if rewards are small (~bps), PPO handles it, but you can normalize returns per-episode to stabilize.
- Episode length: one pass through the historical window = one episode; shuffle start years during training for robustness.
5.9 Mental model (one more time)
Small state → simple action → bounded trade → honest reward. With this environment in place, training PPO is straightforward.
6. Reward & Costs
This section pins down exactly what the agent optimizes each week—in plain English first, then with clean math and drop-in code. Getting this right is the difference between a pretty backtest and a tradable one.
6.1 What the reward measures (in words)
At each decision Friday $t$:
-
The agent chooses an action (follow one expert or HOLD last week’s portfolio).
-
We execute that choice with a turnover cap so trades can’t be too large.
-
One week later ($t{+}1$) we compute:
- Portfolio P&L from the executed weights.
- Transaction cost proportional to how much we traded.
- A small turnover penalty (shapes behavior even if costs are tiny).
- An optional HOLD bonus when a simple stress rule is true (rewarding “do less” in bad regimes).
The net of those is the reward. No look-ahead: nothing from $t{+}1$ is used to decide at $t$; it’s only used to score.
6.2 The reward formula (clean math)
Let:
- $w_t \in \mathbb{R}^{N}$ be the executed weights at $t$ (over the tradable assets, cash handled separately).
- $r_{t+1} \in \mathbb{R}^{N}$ be next week’s simple returns.
- $\text{turnover}t = |w_t - w{t-1}|1 = \sum_i |w{t,i} - w_{t-1,i}|$.
- $c_{\text{bps}}$ be the cost rate (e.g., 2 bps $\Rightarrow$ $c_{\text{bps}}{=}\tfrac{2}{10{,}000}$).
- $\kappa$ be an extra turnover penalty (dimensionless).
- $\text{stress}_t \in {0,1}$ be a binary stress flag based only on week-$t$ information (e.g., SPY$_t{<}{-}1%$ and IEF$_t{>}0.3%$).
- $b_{\text{hold}}$ be the small HOLD bonus (e.g., $5!\times!10^{-4}$).
Then the step reward is:
\boxed{
r_{t+1} =
\underbrace{w_t^\top r_{t+1}}_{\text{next-week PnL}}
\;-\;
\underbrace{c_{\text{bps}}\cdot \text{turnover}_t}_{\text{transaction cost}}
\;-\;
\underbrace{\kappa\cdot \text{turnover}_t}_{\text{turnover penalty}}
\;+\;
\underbrace{b_{\text{hold}}\cdot \mathbf{1}\{\text{stress}_t \land a_t=\text{HOLD}\}}_{\text{optional HOLD bonus}}
}
Units: P&L and penalties are in return space (e.g., +0.004 = +40 bps for the week).
6.3 Optional: a gentle drawdown penalty (two safe variants)
If you want the agent to explicitly prefer smoother equity curves, add a small penalty tied to drawdown—without introducing leakage.
Variant A — Penalize new drawdown only
Maintain cumulative equity $E_t = \prod_{\tau\le t}(1 + w_\tau^\top r_{\tau+1})$. Let $P_t=\max_{\tau\le t} E_\tau$ (running peak), and $\text{DD}_t = 1 - \frac{E_t}{P_t}$.
Penalize the increase in drawdown this step:
r_{t+1}^{(\text{dd})}
= r_{t+1} \;-\; \lambda_{\text{dd}}\cdot \max\!\big(0,\; \text{DD}_{t+1} - \text{DD}_{t}\big).
- Pros: only fires when you make drawdown worse.
- Tip: start tiny, e.g. $\lambda_{\text{dd}} \in [5!\times!10^{-3}, 5!\times!10^{-2}]$.
Variant B — Penalize downside returns (Sortino-like shaping)
Let $r_{t+1}^{\text{net}}$ be the reward before this penalty. Add:
r_{t+1}^{(\text{sortino})}
= r_{t+1} \;-\; \lambda_{-}\cdot \big(\min(0, r_{t+1}^{\text{net}})\big)^2.
- Pros: smooth, local; no stateful equity tracking needed.
- Tip: $\lambda_{-}$ small (e.g., $0.1$–$1.0$) depending on reward scale.
Avoid penalties that look into future tails (e.g., CVaR over the next month)—that leaks information.
6.4 How the stress rule works (and how to change it)
A simple weekly stress flag is plenty to make HOLD meaningful:
stress_t = 1 if (SPY weekly return at t < -1.0%) AND (IEF weekly return at t > +0.3%)
= 0 otherwise
- Reads as: “equities down hard, intermediate Treasuries up”—a risk-off shock.
- Tweak thresholds for your universe; keep it binary and week-t only.
- The HOLD bonus is a small nudge, not a free lunch—costs and caps still apply.
6.5 Putting it into code (drop-in snippet)
This mirrors the environment’s step():
# Inputs for step t (already computed):
# w_prev: pd.Series last executed weights (tickers only, no CASH)
# w_exec: pd.Series executed weights this week (tickers only)
# R_tp1 : pd.Series next-week returns for tickers
# stress_t: bool (computed from week-t info)
# action: int (12 => HOLD; 0..11 => specific expert)
# hyperparams:
c_bps = 2.0 / 10000.0 # 2 bps
kappa = 0.002 # extra turnover penalty
b_hold = 0.0005 # small hold bonus
turnover = float((w_exec - w_prev).abs().sum())
pnl = float((w_exec * R_tp1).sum())
cost = c_bps * turnover
hold_bonus = (b_hold if (stress_t and action == 12) else 0.0)
reward = pnl - cost - kappa * turnover + hold_bonus
With “new drawdown” penalty:
# Maintain these across steps:
# equity_t, peak_t = 1.0, 1.0 (init once per episode)
equity_tp1 = equity_t * (1.0 + pnl) # use net pnl before dd penalty
peak_tp1 = max(peak_t, equity_tp1)
dd_t = 1.0 - equity_t / peak_t
dd_tp1 = 1.0 - equity_tp1 / peak_tp1
lambda_dd = 0.02
reward_dd = reward - lambda_dd * max(0.0, dd_tp1 - dd_t)
# advance state
equity_t, peak_t = equity_tp1, peak_tp1
6.6 Choosing sensible hyperparameters (start here)
| Parameter | Meaning | Typical start | Notes |
|---|---|---|---|
| $c_{\text{bps}}$ | Trading cost per unit turnover | 2 bps | Stress-test at 5–10 bps. |
| $\kappa$ | Extra turnover penalty | 0.002 | Shapes behavior even when $c_{\text{bps}}$ small. |
| $b_{\text{hold}}$ | HOLD bonus under stress | 0.0005 | Keep small; it’s a nudge, not a rule. |
| cap$_\text{turn}$ | L1 turnover cap per step | 20% | Key guardrail; lower → smoother, slower. |
| $\lambda_{\text{dd}}$ | Drawdown penalty weight (Variant A) | 0.02 | Tune 0.005–0.05 if you enable it. |
Tuning tip: pick values on the validation year (e.g., 2019) using Sharpe (and Sortino if you care about downside), not just return.
6.7 Why include both cost and turnover penalty?
- The cost term models market reality (slippage/fees).
- The turnover penalty is shaping: it makes the policy prefer smaller moves even when costs are low or zero, improving stability and capacity.
- They are additive but not redundant: removing $\kappa$ often increases jitter without improving net outcomes.
6.8 Sanity checks (put these in tests)
- No leakage: the only $t{+}1$ thing used at step $t$ is $r_{t+1}$ to score reward.
- HOLD logic: when action is HOLD, $w_t = w_{t-1}$ before turnover cap (which then does nothing).
- Cost units: if $c_{\text{bps}}=2$, trading the entire book (turnover $=1$) costs 0.0002 (2 bps) that week.
- Bounds: weights non-negative; per-asset cap holds; $\sum w_{t,i} \le 1$ (cash soaks the rest).
- Stress flag: depends only on week-$t$ data; confirm with an assertion during training.
6.9 Behavior you should expect (rules of thumb)
- With $\kappa>0$ and a 20% cap, the agent will switch less often and blend toward targets over a few weeks.
- HOLD gets real usage in jagged regimes (and should decline in smooth trends).
- Enabling a small drawdown penalty often reduces tail risk at a modest cost to headline return—watch Sortino and CVaR.
6.10 One-paragraph takeaway
Your reward is next-week net P&L with costs and caps baked in, plus an optional nudge to do nothing during stress. If you want smoother equity, add a gentle drawdown penalty that only fires when drawdown worsens. Keep parameters small and honest, tune on a validation year, and never let week $t{+}1$ information influence decisions at $t$.
7. Training the PPO Meta-Controller
In this section we’ll (a) set up train / validation / OOS splits, (b) define a reproducible PPO config, (c) run a small LR sweep and pick the best by validation Sharpe, and (d) save everything you need for later evaluation.
7.1 Data splits (keep them fixed and explicit)
We’ll use weekly data (from Section 3) and the experts cache (from Section 4):
Train: 2010-01-01 → 2018-12-31
Validation: 2019-01-01 → 2019-12-31
OOS Test: 2020-01-01 → 2025-09-01
Why: training needs years of variety, validation is a single clean year for hyperparameter selection, and OOS is untouched until the very end.
7.2 Reproducibility (seed everything)
import os, random, numpy as np
import torch
SEED = 42
random.seed(SEED)
np.random.seed(SEED)
torch.manual_seed(SEED)
os.environ["PYTHONHASHSEED"] = str(SEED)
Stable-Baselines3 will also receive this seed to initialize its own RNGs.
7.3 Build split-specific environments
You’ll slice the weekly returns and expert weights by date. The env is the MetaAllocatorEnv from Section 5.
import pandas as pd
from stable_baselines3.common.env_util import make_vec_env
from stable_baselines3.common.vec_env import VecMonitor
# Helpers
def slice_by_dates(df, start, end):
return df.loc[(df.index >= start) & (df.index <= end)]
def slice_experts(experts_weights: dict, start, end):
out = {}
for name, df in experts_weights.items():
out[name] = slice_by_dates(df, start, end)
return out
# Date ranges
TRN0, TRN1 = "2010-01-01", "2018-12-31"
VAL0, VAL1 = "2019-01-01", "2019-12-31"
OOS0, OOS1 = "2020-01-01", "2025-09-01"
# Sliced data
R_train = slice_by_dates(weekly_rets, TRN0, TRN1)
R_valid = slice_by_dates(weekly_rets, VAL0, VAL1)
R_oos = slice_by_dates(weekly_rets, OOS0, OOS1)
EXP_TRN = slice_experts(experts_weights, TRN0, TRN1)
EXP_VAL = slice_experts(experts_weights, VAL0, VAL1)
EXP_OOS = slice_experts(experts_weights, OOS0, OOS1)
# expert_perf dict (name -> Series of realized next-week returns per Section 4.5)
PERF_TRN = expert_perf_train # built once using the train+val date index
PERF_VAL = expert_perf_valid
PERF_OOS = expert_perf_oos
Create vectorized envs (1–4 copies is enough at weekly cadence)
def make_env_fn(R, EXP, PERF):
def _fn():
return MetaAllocatorEnv(
weekly_rets=R,
experts_weights=EXP,
expert_perf=PERF,
tickers=TICKERS,
trade_cost_bps=2.0,
kappa_turnover=0.002,
hold_bonus=0.0005,
turnover_cap=0.20
)
return _fn
train_env = make_vec_env(make_env_fn(R_train, EXP_TRN, PERF_TRN),
n_envs=2, seed=SEED)
train_env = VecMonitor(train_env, filename=None)
# For validation we use a single, monitored env (no learning)
valid_env = make_vec_env(make_env_fn(R_valid, EXP_VAL, PERF_VAL),
n_envs=1, seed=SEED)
valid_env = VecMonitor(valid_env, filename=None)
We keep things simple: no reward normalization (finance rewards already carry meaningful scale). If you normalize observations, remember to save and reuse the scaler at eval time.
7.4 PPO configuration (good starting point)
We’ll use a small MLP and conservative PPO settings that work well with weekly rewards.
from stable_baselines3 import PPO
from stable_baselines3.common.torch_layers import BaseFeaturesExtractor
from torch import nn
policy_kwargs = dict(
activation_fn=nn.ReLU,
net_arch=dict(pi=[1024, 512], vf=[1024, 512]), # policy & value nets
ortho_init=False
)
ppo_common = dict(
policy="MlpPolicy",
n_steps=2048, # ≥ episode length is NOT required; PPO handles truncation
batch_size=256,
n_epochs=10,
gamma=0.99,
gae_lambda=0.95,
ent_coef=0.005, # small exploration
clip_range=0.30, # allow moderate updates
vf_coef=0.5,
max_grad_norm=0.5,
target_kl=0.20, # stop aggressive policy updates
tensorboard_log="./tb/",
seed=SEED,
policy_kwargs=policy_kwargs,
verbose=1
)
These are defaults that behave well. You’ll only sweep learning rate to keep selection simple and honest.
7.5 Validation metric (pick the LR by Sharpe on validation)
We select the learning rate by the validation Sharpe of net-of-cost weekly returns (exclude shaping terms like the turnover penalty or HOLD bonus).
We’ll evaluate via a helper that rolls the env once, logging per-step pnl, cost, turnover, and reward. (If your env’s step() doesn’t expose these in info, add them—see the note in Section 5.)
import numpy as np
def eval_on_env(model, env, ann_factor=52):
obs, info = env.reset()
pnl_series, cost_series = [], []
done, truncated = False, False
while True:
action, _ = model.predict(obs, deterministic=True)
obs, reward, done, truncated, info = env.step(action)
# expect VecMonitor -> info is a list (one env)
info0 = info[0]
# Your env should put these in info; if not, extend it:
# info0["pnl"], info0["cost"]
if "pnl" in info0 and "cost" in info0:
pnl_series.append(info0["pnl"] - info0["cost"]) # net-of-cost
else:
# fallback: use reward (includes shaping) if you didn't expose components
pnl_series.append(float(reward[0]))
if done[0] or truncated[0]:
break
r = np.array(pnl_series, dtype=float)
mu, sd = r.mean(), r.std(ddof=1) + 1e-12
sharpe = (mu * ann_factor) / (sd * np.sqrt(ann_factor))
return dict(
mean=mu, std=sd, sharpe=sharpe,
n=len(r), series=r
)
7.6 Learning-rate sweep (train → validate → pick best)
LR_GRID = [1e-4, 3e-4, 1e-3]
TIMESTEPS = 400_000
results = []
best = None
for lr in LR_GRID:
model = PPO(env=train_env, learning_rate=lr, **ppo_common)
model.learn(total_timesteps=TIMESTEPS, progress_bar=False)
# Validate
val_metrics = eval_on_env(model, valid_env)
result = dict(lr=lr, **val_metrics)
results.append(result)
# Save checkpoint per LR
model_path = f"models/ppo_lr{lr:.0e}.zip"
model.save(model_path)
# Track best by validation Sharpe
if best is None or val_metrics["sharpe"] > best["sharpe"]:
best = dict(lr=lr, path=model_path, **val_metrics)
# Save a copy as the canonical "best" model
import shutil, os
os.makedirs("models", exist_ok=True)
best_path = "models/ppo_best.zip"
shutil.copyfile(best["path"], best_path)
print("Best LR:", best["lr"], "Val Sharpe:", round(best["sharpe"], 3))
Keep the sweep tiny (2–3 LRs). The goal is robustness, not over-optimization.
7.7 Optional: callbacks & TensorBoard
Add evaluation during training and early stopping safeguards:
from stable_baselines3.common.callbacks import EvalCallback, StopTrainingOnNoModelImprovement, CallbackList
stop_no_improve = StopTrainingOnNoModelImprovement(
max_no_improvement_evals=5, min_evals=5, verbose=1
)
eval_cb = EvalCallback(
eval_env=valid_env,
best_model_save_path="models/best_tmp",
log_path="models/eval_logs",
eval_freq=10_000, # every N env steps
deterministic=True,
callback_after_eval=stop_no_improve
)
model = PPO(env=train_env, learning_rate=best["lr"], **ppo_common)
model.learn(total_timesteps=TIMESTEPS, callback=CallbackList([eval_cb]), progress_bar=False)
model.save("models/ppo_best.zip")
Launch TensorBoard to monitor losses, explained variance, entropy, and KL. (Exact commands depend on your platform.)
7.8 Save what matters (so evaluation is plug-and-play)
models/ppo_best.zip— the trained policy.- Any observation scaler (if you used one).
- The experts cache and weekly returns Parquets (already saved).
- A small
config.yamlwith dates, costs, caps, and seed.
Example:
model: models/ppo_best.zip
seed: 42
dates:
train: [2010-01-01, 2018-12-31]
valid: [2019-01-01, 2019-12-31]
oos: [2020-01-01, 2025-09-01]
costs:
trade_cost_bps: 2.0
kappa_turnover: 0.002
hold_bonus: 0.0005
caps:
turnover_cap: 0.20
max_per_asset: 0.35
obs:
normalized: false
7.9 Sanity checks before moving on
- Learning signal present: training entropy should decrease slowly; value loss bounded; KL near
target_kl. - No leakage: evaluation code never uses week $t{+}1$ features to decide at $t$.
- Validation Sharpe is computed on net-of-cost weekly returns (not raw reward if you used shaping terms).
- Stable behavior: action usage isn’t collapsing to a single expert from step 1 (unless that’s truly optimal).
7.10 Common pitfalls (and quick fixes)
- Exploding updates (policy collapses): lower
clip_range(0.2), settarget_klsmaller (0.10), or reduce LR. - No exploration (stuck on HOLD): increase
ent_coefslightly (0.007–0.01) or widenclip_rangea bit. - High churn despite penalties: increase
kappa_turnoveror reduceturnover_capto 10–15%. - Validation beats train oddly: check that your state features are using only past data and that your expert weights at time $t$ don’t peek into $t{+}1$.
7.11 Minimal “one-shot” script
This script wraps everything above so you can train and select the best LR in one go.
def train_select_save(lr_grid=(1e-4, 3e-4, 1e-3), timesteps=400_000):
best = None
for lr in lr_grid:
model = PPO(env=train_env, learning_rate=lr, **ppo_common)
model.learn(total_timesteps=timesteps, progress_bar=False)
metrics = eval_on_env(model, valid_env)
path = f"models/ppo_lr{lr:.0e}.zip"
model.save(path)
cand = dict(lr=lr, path=path, **metrics)
if best is None or cand["sharpe"] > best["sharpe"]:
best = cand
# keep the winner
import shutil, os
os.makedirs("models", exist_ok=True)
shutil.copyfile(best["path"], "models/ppo_best.zip")
return best
best = train_select_save()
print("Selected LR:", best["lr"], "Sharpe:", round(best["sharpe"], 3))
7.12 What to remember
- Keep the model small and the sweep tiny (just LR).
- Pick the winner by validation Sharpe of net-of-cost weekly returns.
- Save the model + config + caches so OOS evaluation is painless.
8. Baselines & Metrics
To trust your PPO meta-controller, you need simple, transparent baselines and a clean metrics suite. This section gives you both—implemented in a way that’s fair (same costs, same caps, same turnover limits) and easy to reuse.
8.1 Why baselines (and what “fair” means here)
- Equal Weight (1/N): diversification with zero bells & whistles.
- 60/40: the classic risk-on/risk-off split.
- Best Single Expert: always follow the one HRP/HERC expert chosen on validation.
- Random Switcher: uniformly pick among experts + HOLD (a sanity check).
Fairness rules: every strategy uses the same execution engine:
- Per-asset cap: 35%
- Turnover cap: 20% L1 per week
- Cash allowance: up to 5% if caps prevent full investment
- Trading cost: 2 bps per unit turnover
- Weekly decisions: act at $t$, realize P&L at $t{+}1$
8.2 A common execution wrapper (plug any target weights into this)
All baselines reduce to: “produce target weights $w_t^*$ at each $t$, then execute with caps, turnover limit, and costs.”
import numpy as np, pandas as pd
def execute_backtest(weekly_rets: pd.DataFrame,
target_weights_fn,
tickers: list,
max_per_asset=0.35,
turnover_cap=0.20,
trade_cost_bps=2.0,
w0: pd.Series = None):
"""
Run a strategy by repeatedly calling target_weights_fn(t) -> desired weights for date t,
then executing with per-asset caps, turnover cap, and trading costs.
Returns a dict with time series (net, gross, cost, turnover) and final weights.
"""
dates_t = weekly_rets.index[:-1]
dates_tp1 = weekly_rets.index[1:]
c_bps = trade_cost_bps / 10000.0
# init portfolio
if w0 is None:
w_prev = pd.Series(1.0/len(tickers), index=tickers) # equal-weight start
else:
w_prev = w0.reindex(tickers).fillna(0.0)
out = {
"net": [], "gross": [], "cost": [], "turnover": [],
"date": [], "w_exec": []
}
for t, tp1 in zip(dates_t, dates_tp1):
# 1) get target weights for this date (tickers only)
w_target = target_weights_fn(t).reindex(tickers).fillna(0.0)
# 2) per-asset cap (long-only), renormalize if needed
w_cap = w_target.clip(lower=0.0, upper=max_per_asset)
s = float(w_cap.sum())
if s > 1.0: # re-scale down if caps overfilled
w_cap = w_cap / s
s = 1.0
# small optional cash if under-invested after caps
cash = max(0.0, min(0.05, 1.0 - s))
# 3) turnover-capped execution between last & target
delta = w_cap - w_prev
l1 = float(np.abs(delta).sum())
if l1 > turnover_cap + 1e-12:
delta *= (turnover_cap / l1)
w_exec = (w_prev + delta).clip(lower=0.0)
# renormalize tiny drift (keep simple)
if w_exec.sum() > 1.0:
w_exec /= float(w_exec.sum())
# 4) compute P&L, cost, net
gross = float((w_exec.values * weekly_rets.loc[tp1, tickers].values).sum())
turnover = float(np.abs(w_exec - w_prev).sum())
cost = c_bps * turnover
net = gross - cost
# 5) record & advance
out["date"].append(tp1)
out["gross"].append(gross)
out["cost"].append(cost)
out["net"].append(net)
out["turnover"].append(turnover)
out["w_exec"].append(w_exec)
w_prev = w_exec
for k in ["net","gross","cost","turnover"]:
out[k] = pd.Series(out[k], index=out["date"], name=k)
out["weights"] = pd.DataFrame(out["w_exec"], index=out["date"])
return out
8.3 Baseline #1 — Equal Weight (1/N)
Target rule: each week, $w_t^* = \frac{1}{N}$ on all tickers (before caps). Caps/turnover/costs are applied by the execution wrapper.
def target_eqw(t):
return pd.Series(1.0/len(TICKERS), index=TICKERS)
eqw_run = execute_backtest(weekly_rets, target_eqw, TICKERS)
Note: Because of the turnover cap, the executed weights converge gradually to 1/N from the initial portfolio.
8.4 Baseline #2 — 60/40 (two sensible variants)
Variant A (SPY/TLT only): classic 60% SPY, 40% TLT as the target. Per-asset caps may bind (e.g., SPY capped at 35%), with any leftover going to cash.
def target_6040_spy_tlt(t):
w = pd.Series(0.0, index=TICKERS)
w["SPY"] = 0.60
w["TLT"] = 0.40
return w
b6040_A = execute_backtest(weekly_rets, target_6040_spy_tlt, TICKERS)
Variant B (sleeve-aware to avoid cap binding): allocate 60% to equity sleeve (SPY, IEFA, EEM equally) and 40% to duration sleeve (IEI, IEF, TLT equally). This keeps per-asset weights ≤ 35% while preserving the 60/40 spirit.
EQ = ["SPY","IEFA","EEM"]
DUR = ["IEI","IEF","TLT"]
def target_6040_sleeves(t):
w = pd.Series(0.0, index=TICKERS)
w[EQ] = 0.60 / len(EQ)
w[DUR] = 0.40 / len(DUR)
return w
b6040_B = execute_backtest(weekly_rets, target_6040_sleeves, TICKERS)
Pick one for your report; the sleeve variant reads better under position caps.
8.5 Baseline #3 — Best Single Expert (chosen on validation)
- Choose the winner on the validation year (2019): the expert with the highest validation Sharpe computed using the same execution engine (its targets change week to week as the expert re-optimizes).
- Lock it in and run OOS with that one expert.
def make_expert_target_fn(expert_weights_df):
def _fn(t):
return expert_weights_df.loc[t].reindex(TICKERS).fillna(0.0)
return _fn
# 1) score each expert on validation
val_scores = []
for name, df in EXP_VAL.items(): # EXP_VAL: {expert_name -> weights DF on validation dates}
run = execute_backtest(R_valid, make_expert_target_fn(df), TICKERS)
s = run["net"]; mu, sd = s.mean(), s.std(ddof=1) + 1e-12
sharpe_val = (mu * 52) / (sd * np.sqrt(52))
val_scores.append((name, sharpe_val))
best_expert = max(val_scores, key=lambda x: x[1])[0]
# 2) run OOS with the chosen expert
best_run = execute_backtest(R_oos, make_expert_target_fn(EXP_OOS[best_expert]), TICKERS)
This baseline is strong: it benefits from weekly re-optimization inside the expert, but does not get to switch between experts.
8.6 Baseline #4 — Random Switcher (experts + HOLD)
Uniformly pick one of the 12 experts or HOLD each week, then execute.
import random
EXPERT_NAMES = list(EXP_OOS.keys())
def target_random_switch(t):
# 12 experts + HOLD
choices = EXPERT_NAMES + ["HOLD"]
pick = random.choice(choices)
if pick == "HOLD":
# Signal to wrapper: “stay where you are” by returning the previous executed weights.
# If your wrapper doesn’t track that, return a copy of last exec weights externally.
return last_exec_weights.copy() # <-- implement in your loop
else:
return EXP_OOS[pick].loc[t].reindex(TICKERS).fillna(0.0)
In practice, implement RANDOM inside a custom loop so you can access
last_exec_weights. The goal is a true do-nothing HOLD, not “rebuild last week’s portfolio” (which would still incur costs).
8.7 Metrics (definitions you can trust)
Let $r_t$ be the weekly net-of-cost return series (length $n$). We use $A=52$ weeks/year.
-
Geometric annual return
$$ \text{AnnRet} = \Big(\prod_{t=1}^n (1+r_t)\Big)^{A/n} - 1. $$
-
Sharpe (annualized, 0% rf)
$$ \text{Sharpe} = \frac{\bar r \cdot A}{\sigma_r \sqrt{A}},\quad \bar r = \frac{1}{n}\sum r_t,\ \sigma_r = \text{stdev}(r_t). $$
-
Sortino (annualized, 0% target)
$$ \text{Sortino} = \frac{\bar r \cdot A}{\sigma_{-} \sqrt{A}},\quad \sigma_{-} = \sqrt{\tfrac{1}{n}\sum \big(\min(0,r_t)\big)^2 }. $$
-
CVaR@5% (Expected Shortfall) Sort $r_t$; let $Q$ be the 5th percentile.
$$ \text{CVaR}_{5%} = \text{mean}{, r_t : r_t \le Q ,}. $$
(More negative = worse tails.)
-
Max Drawdown (from equity curve $E_t=\prod_{\tau\le t}(1+r_\tau)$)
$$ \text{MaxDD} = \max_t \Big(1 - \frac{E_t}{\max_{\tau \le t} E_\tau}\Big). $$
-
Turnover (average weekly L1)
$$ \overline{\text{TO}} = \frac{1}{n}\sum |w_t - w_{t-1}|_1. $$
-
Cost drag (annualized) ≈ $A \cdot \overline{\text{cost}_t}$, where $\text{cost}t = c{\text{bps}}\cdot\text{turnover}_t$.
8.8 Metrics implementation (drop-in)
def metrics_from_run(run, ann_factor=52):
# run: dict from execute_backtest
r = run["net"].astype(float) # weekly net-of-cost returns
gross = run["gross"].astype(float)
cost = run["cost"].astype(float)
to = run["turnover"].astype(float)
# annualized return (geometric)
eq = (1.0 + r).cumprod()
ann_ret = eq.iloc[-1]**(ann_factor/len(r)) - 1.0
# sharpe/sortino
mu = r.mean(); sd = r.std(ddof=1) + 1e-12
sharpe = (mu * ann_factor) / (sd * np.sqrt(ann_factor))
downside = np.minimum(0.0, r).pow(2).mean()**0.5
sortino = (mu * ann_factor) / (downside * np.sqrt(ann_factor) + 1e-12)
# cvar@5
q05 = r.quantile(0.05)
cvar5 = r[r <= q05].mean()
# max drawdown
eq_curve = (1.0 + r).cumprod()
peak = eq_curve.cummax()
dd = 1.0 - (eq_curve / peak)
maxdd = dd.max()
# turnover & cost drag
avg_to = to.mean()
cost_drag = cost.mean() * ann_factor
return {
"AnnRet": float(ann_ret),
"Sharpe": float(sharpe),
"Sortino": float(sortino),
"CVaR5": float(cvar5),
"MaxDD": float(maxdd),
"Turnover": float(avg_to),
"CostDrag": float(cost_drag),
"N": int(len(r))
}
8.9 Putting it together (evaluation table)
After you’ve run your PPO and each baseline on the same OOS window:
rows = []
rows.append(("PPO Switcher", metrics_from_run(ppo_run)))
rows.append(("Equal Weight", metrics_from_run(eqw_run)))
rows.append(("60/40 (SPY/TLT)", metrics_from_run(b6040_A))) # or sleeve variant
rows.append(("Best Expert", metrics_from_run(best_run)))
rows.append(("Random", metrics_from_run(random_run)))
tbl = pd.DataFrame({name: m for name, m in rows}).T[["AnnRet","Sharpe","Sortino","CVaR5","MaxDD","Turnover","CostDrag","N"]]
print(tbl.round(3))
Template for your post:
| Strategy | Ann. Ret | Sharpe | Sortino | CVaR@5% | MaxDD | Turnover | Cost Drag |
|------------------|----------|--------|---------|---------|-------|----------|-----------|
| PPO Switcher | | | | | | | |
| Equal Weight | | | | | | | |
| 60/40 (SPY/TLT) | | | | | | | |
| Best Expert | | | | | | | |
| Random | | | | | | | |
8.10 Sanity checks (don’t skip)
- Same frictions everywhere: caps, turnover cap, and costs are identical across PPO and baselines.
- HOLD semantics: for RANDOM, HOLD truly preserves last week’s weights (no hidden trading).
- Annualization: always treat the series as weekly (52) unless you’ve changed cadence.
- MaxDD: compute from cumulative net equity, not from raw returns.
- Best Expert selection: chosen only on validation, not peeked from OOS.
8.11 One-paragraph takeaway
Baselines make results legible. With a common execution wrapper, you can compare PPO against 1/N, 60/40, a strong fixed expert, and a random switcher—all under the same costs and caps. The metrics—Ann. Return, Sharpe, Sortino, CVaR@5%, MaxDD, Turnover, Cost Drag—tell a complete story: efficiency, tails, and tradability.
9. Results (Out-of-Sample)
This is where everything comes together. We’ll (a) plot equity curves and drawdowns, (b) look at turnover and action usage, (c) break performance by stress vs. non-stress weeks, and (d) summarize what the plots actually mean.
All code below assumes you’ve already produced the OOS runs from Section 8:
ppo_run,eqw_run,b6040_run(pick your 60/40 variant),best_run,random_run- Each is a dict from
execute_backtest(...)with keys:net,gross,cost,turnover,weights(weekly, indexed by dates).
9.1 What we’ll visualize
- Equity curves (net of costs): PPO vs. baselines on the same axis.
- Drawdown curve (PPO): peak-to-trough % from the net equity curve.
- Turnover histogram: how much the strategy trades each week.
- Action timeline (PPO): which expert (or HOLD) the agent chose each week.
- Regime breakdown: performance in stress vs non-stress weeks.
Use these to answer: Is the agent stable? When does it HOLD? Are tails better? Is turnover tradable?
9.2 Equity curves (net of costs)
import pandas as pd
import matplotlib.pyplot as plt
def equity(net_series: pd.Series) -> pd.Series:
"""Net-of-cost equity curve starting at 1.0."""
return (1.0 + net_series).cumprod()
curves = pd.DataFrame({
"PPO": equity(ppo_run["net"]),
"EqualWeight":equity(eqw_run["net"]),
"60/40": equity(b6040_run["net"]),
"BestExpert": equity(best_run["net"]),
"Random": equity(random_run["net"])
}).dropna(how="all")
ax = curves.plot(figsize=(10,5), title="OOS Equity Curves (Net of Costs)")
ax.set_ylabel("Cumulative Net (×)")
ax.set_xlabel("Date")
plt.tight_layout()
# savefig optional: plt.savefig("outputs/figures/equity_curves.png", dpi=150)
How to read it:
- Look for big separations during major periods (e.g., 2020 crash, 2022 bond selloff).
- Flat vs. jagged segments hint at HOLD usage or cap-limited moves.
Rule of thumb: a “quiet” but steadily rising curve often beats a taller but jagged one once you factor MaxDD, CVaR, and turnover.
9.3 Drawdown curve (PPO)
ppo_eq = equity(ppo_run["net"])
ppo_peak = ppo_eq.cummax()
ppo_dd = 1.0 - (ppo_eq / ppo_peak)
ax = ppo_dd.plot(figsize=(10,3), title="PPO Drawdown (OOS)")
ax.set_ylabel("Drawdown")
ax.set_xlabel("Date")
plt.tight_layout()
# plt.savefig("outputs/figures/ppo_drawdown.png", dpi=150)
How to read it:
- Depth: worst trough = MaxDD.
- Duration: time to recover to a new high.
- Long, shallow drawdowns are often more livable than short, deep ones.
9.4 Turnover histogram
import numpy as np
turnovers = pd.DataFrame({
"PPO": ppo_run["turnover"],
"EqualWeight":eqw_run["turnover"],
"60/40": b6040_run["turnover"],
"BestExpert": best_run["turnover"],
"Random": random_run["turnover"],
})
ax = turnovers["PPO"].plot(kind="hist", bins=20, alpha=0.6, figsize=(8,4),
title="PPO Weekly Turnover Distribution (OOS)")
ax.set_xlabel("L1 Turnover per Week")
plt.tight_layout()
# plt.savefig("outputs/figures/ppo_turnover_hist.png", dpi=150)
How to read it:
- Mass near 0.00–0.05 → gentle, capacity-friendly.
- Spikes near your cap (e.g., 0.20) mean the strategy wants to move faster than allowed—note how often that happens.
Quick “cap-hit” estimate:
cap = 0.20
cap_hits = (np.isclose(ppo_run["turnover"], cap, atol=1e-6) | (ppo_run["turnover"] > cap - 1e-6)).mean()
print(f"Approx. % of weeks at turnover cap: {cap_hits:.1%}")
9.5 Action usage timeline (PPO)
Log which expert (or HOLD) the agent chose each week. If you didn’t record actions during evaluation, re-run a deterministic OOS roll to capture them:
# Pseudocode: step a fresh OOS env once and record actions.
# Assumes you have: `oos_env = MetaAllocatorEnv(...)` and `ppo_model` loaded.
acts, dates = [], []
obs, info = oos_env.reset()
done = False
while not done:
a, _ = ppo_model.predict(obs, deterministic=True)
acts.append(int(a))
dates.append(info["date"])
obs, reward, done, truncated, info = oos_env.step(a)
actions = pd.Series(acts, index=dates, name="action")
# Map IDs to labels (keep consistent with Section 5)
ACTION_LABELS = {
0:"HRP-60",1:"HRP-120",2:"HRP-252",3:"HRP-504",4:"HRP-756",5:"HRP-1008",
6:"HERC-60",7:"HERC-120",8:"HERC-252",9:"HERC-504",10:"HERC-756",11:"HERC-1008",
12:"HOLD"
}
labels = actions.map(ACTION_LABELS)
# Plot as a categorical timeline (one row per week)
fig, ax = plt.subplots(figsize=(10, 2.8))
ax.scatter(labels.index, labels.map({k:i for i,k in enumerate(sorted(set(labels)))}), s=8)
ax.set_yticks(range(len(sorted(set(labels)))))
ax.set_yticklabels(sorted(set(labels)))
ax.set_title("PPO Action Timeline (OOS)")
ax.set_xlabel("Date")
plt.tight_layout()
# plt.savefig("outputs/figures/ppo_actions_timeline.png", dpi=150)
What to look for:
- HOLD % over OOS.
- Clusters of similar experts during persistent regimes.
- Flip-flop in choppy periods (ideally rare if costs/penalties/caps are set right).
HOLD share:
hold_pct = (labels == "HOLD").mean()
print(f"HOLD usage: {hold_pct:.1%} of OOS weeks")
9.6 Regime breakdown (stress vs. non-stress)
Use the weekly stress rule from Section 6 (e.g., SPY↓ & IEF↑) to segment results.
def stress_flag(weekly_rets: pd.DataFrame) -> pd.Series:
spy = weekly_rets["SPY"]
ief = weekly_rets["IEF"]
return (spy < -0.01) & (ief > 0.003)
oos_idx = ppo_run["net"].index # OOS dates
stress = stress_flag(weekly_rets).reindex(oos_idx).fillna(False)
def mean_std Sharpe(r, A=52):
mu, sd = r.mean(), r.std(ddof=1) + 1e-12
return mu, sd, (mu*A)/(sd*np.sqrt(A))
def regime_report(run, name):
r = run["net"].reindex(oos_idx)
mu_s, sd_s, sh_s = mean_stdSharpe(r[stress])
mu_n, sd_n, sh_n = mean_stdSharpe(r[~stress])
print(f"{name:12} | Stress μ={mu_s:.4f} σ={sd_s:.4f} Sharpe={sh_s:.2f} "
f"| Non-stress μ={mu_n:.4f} σ={sd_n:.4f} Sharpe={sh_n:.2f}")
for nm, rn in [("PPO", ppo_run), ("EqW", eqw_run), ("60/40", b6040_run), ("BestExp", best_run)]:
regime_report(rn, nm)
# HOLD usage in stress vs non-stress (PPO only, needs action labels aligned to oos_idx)
hold_stress = (labels.reindex(oos_idx)[stress] == "HOLD").mean()
hold_non = (labels.reindex(oos_idx)[~stress] == "HOLD").mean()
print(f"HOLD in stress: {hold_stress:.1%} | HOLD in non-stress: {hold_non:.1%}")
How to read it:
- PPO should downshift (more HOLD, gentler trading) during stress.
- Compare stress-period Sharpe and mean returns to EqW/60-40: does PPO avoid the worst weeks?
9.7 One compact metrics table (reprise)
You built metrics_from_run in Section 8. Use it here to print the OOS summary next to the plots for easy copy-paste into the blog:
import pandas as pd
rows = []
rows.append(("PPO Switcher", metrics_from_run(ppo_run)))
rows.append(("Equal Weight", metrics_from_run(eqw_run)))
rows.append(("60/40", metrics_from_run(b6040_run)))
rows.append(("Best Expert", metrics_from_run(best_run)))
rows.append(("Random", metrics_from_run(random_run)))
tbl = pd.DataFrame({name: m for name, m in rows}).T[["AnnRet","Sharpe","Sortino","CVaR5","MaxDD","Turnover","CostDrag","N"]]
display(tbl.round(3))
# Optionally: tbl.to_csv("outputs/csv/oos_summary.csv")
Use this exact table in your post so readers can scan efficiency (Sharpe/Sortino), tail risk (CVaR/MaxDD), and tradability (Turnover/CostDrag) at a glance.
9.8 Interpreting typical outcomes (reading guide)
- Equity/Drawdown: If PPO’s curve isn’t the tallest but shows a shallower MaxDD and better CVaR, that’s a smoother risk path—often preferable.
- Turnover: If most mass is <10% with occasional cap hits, the behavior is capacity-friendly while still responsive.
- Actions: Healthy PPO behavior shows blocks of the same expert during trends and HOLD in ragged stress pockets—not constant flitting.
- Regimes: Ideally, PPO’s stress-period returns/Sharpe beat EqW/60-40, evidencing the value of the HOLD and the switching.
9.9 Sanity checks before you publish
- Plots use net-of-cost returns (not gross).
- OOS window is never used in training/validation.
- The stress rule uses only week-$t$ info; no peeking.
- HOLD in the PPO rollout truly means “no trade” (turnover ~ 0, barring cap/clip artifacts).
- Metrics table equals what you see in the plots (e.g., MaxDD from the net equity curve).
9.10 One-paragraph takeaway
Your PPO meta-controller should look measured: competitive equity, controlled drawdowns, lower tails, and sensible trading. The action timeline and regime breakdown explain why: the agent leans into robust experts in good times and HOLDs when simple stress signals flash. Together, this makes the behavior interpretable and the backtest believable.
10. Ablations & Diagnostics
This section shows how to test which ingredients actually matter and how to debug behavior. We’ll run small, controlled experiments (ablations) and add diagnostics you can trust.
10.1 What we’ll ablate (and why)
- No Regime Features → Does the agent really use vol/trend/stress or just recent expert performance?
- No HOLD Bonus → If we remove the nudge, will PPO still learn to sit on its hands in stress?
- Add Drawdown Penalty → Does a tiny penalty improve tails without killing returns?
- Mixture-of-Experts (Soft Weights) → Instead of picking one expert, blend them; does it help under a turnover cap?
- Turnover Cap Sensitivity → 10%, 15%, 20%, 30% — how does tradability vs. reactivity trade off?
- Cost Sweep → 2/5/10 bps — is the policy robust to more realistic frictions?
- Walk-Forward vs. Fixed Split → Does retraining each year change the story?
- Reverse-Time Stress Test → Train on later years, test on earlier years — overfitting check.
- Entropy/Clip Sensitivity → Does policy stability depend on these knobs?
- Seed Robustness → Repeat with different RNG seeds (3–5 runs).
- Expert Pool Variants → Remove long lookbacks / short lookbacks / one allocator family (HRP or HERC) to test redundancy.
The goal is clarity, not a grid search. Keep each ablation minimal and compare on the same OOS window with the same evaluation code from Section 8–9.
10.2 Minimal ablation harness (copy-paste)
from dataclasses import dataclass, asdict
import itertools, numpy as np, pandas as pd
@dataclass
class AblationCfg:
name: str
use_regime_features: bool = True
use_hold_bonus: bool = True
dd_penalty_lambda: float = 0.0 # 0 => off
turnover_cap: float = 0.20
trade_cost_bps: float = 2.0
ent_coef: float = 0.005
clip_range: float = 0.30
seed: int = 42
policy_type: str = "discrete" # 'discrete' or 'softmix'
# softmix only:
softmax_temp: float = 1.0
def run_ablation(cfg: AblationCfg):
# 1) build env with flags
env = make_env_with_flags(
weekly_rets=R_train, EXP=EXP_TRN, PERF=PERF_TRN, tickers=TICKERS,
use_regime_features=cfg.use_regime_features,
use_hold_bonus=cfg.use_hold_bonus,
dd_penalty_lambda=cfg.dd_penalty_lambda,
turnover_cap=cfg.turnover_cap,
trade_cost_bps=cfg.trade_cost_bps,
policy_type=cfg.policy_type,
softmax_temp=cfg.softmax_temp,
seed=cfg.seed
)
venv = VecMonitor(make_vec_env(lambda: env, n_envs=2, seed=cfg.seed))
# 2) train PPO with selected entropy/clip
model = PPO("MlpPolicy", venv, learning_rate=best_lr, n_steps=2048, batch_size=256,
ent_coef=cfg.ent_coef, clip_range=cfg.clip_range, seed=cfg.seed,
policy_kwargs=policy_kwargs, verbose=0)
model.learn(total_timesteps=400_000)
# 3) evaluate on OOS
oos_env = make_env_with_flags(
weekly_rets=R_oos, EXP=EXP_OOS, PERF=PERF_OOS, tickers=TICKERS,
use_regime_features=cfg.use_regime_features,
use_hold_bonus=cfg.use_hold_bonus,
dd_penalty_lambda=cfg.dd_penalty_lambda,
turnover_cap=cfg.turnover_cap,
trade_cost_bps=cfg.trade_cost_bps,
policy_type=cfg.policy_type,
softmax_temp=cfg.softmax_temp,
seed=cfg.seed
)
ppo_run = rollout_deterministic(model, oos_env) # returns dict like execute_backtest
metrics = metrics_from_run(ppo_run)
return {**asdict(cfg), **metrics}
make_env_with_flags(...)is your Section-5 env with a fewifswitches;rollout_deterministic(...)is the same evaluation pass you use in Section 9 to record actions/turnover.
10.3 Ablation #1 — Remove Regime Features
Question: Are vol/trend/stress helping beyond recent expert performance?
cfg = AblationCfg(name="no_regime", use_regime_features=False)
res_no_regime = run_ablation(cfg)
What to watch:
- HOLD usage during stress weeks may drop.
- CVaR/MaxDD often worsen slightly; Sharpe may be similar if recent performance features dominate.
10.4 Ablation #2 — Remove HOLD Bonus
Question: Will the policy still learn to HOLD in stress without a nudge?
cfg = AblationCfg(name="no_hold_bonus", use_hold_bonus=False)
res_no_hold = run_ablation(cfg)
Expected: Small drop in HOLD% and slightly higher turnover; tails may worsen in sharp shocks.
10.5 Ablation #3 — Add Gentle Drawdown Penalty
Question: Does a tiny penalty smooth tails?
for lam in [0.005, 0.02, 0.05]:
cfg = AblationCfg(name=f"dd_lambda_{lam}", dd_penalty_lambda=lam)
print(run_ablation(cfg))
Expected: CVaR@5% and MaxDD improve; AnnRet and Sharpe may dip slightly. Pick the knee (e.g., λ≈0.02).
10.6 Ablation #4 — Mixture-of-Experts (Soft Weights)
Idea: Output a simplex over experts (+ HOLD) and blend their target weights, then apply the same turnover cap.
10.6.1 How it works
At week $t$, let $p \in \Delta^{E}$ be softmax logits over E+1 choices (12 experts + HOLD). Let $W^{(e)}t$ be expert $e$’s capped weights, and $w{t-1}$ last week’s executed weights.
Target before execution:
w^\star_t = \sum_{e=1}^{E} p_e \, W^{(e)}_t \;+\; p_{\text{HOLD}} \, w_{t-1}.
Then apply the turnover cap to get $w_t$ and compute reward as usual.
Notes: • If
p_HOLDgets large, the model can “glide” and reduce turnover naturally — that’s okay. • Use a temperatureτin softmax to control sparsity:softmax(logits/τ). Lowerτ→ more peaky (closer to discrete). • Keep the same costs and caps.
10.6.2 Minimal env tweak (action = logits vector)
class MetaAllocatorSoftMixEnv(MetaAllocatorEnv):
def __init__(self, *args, softmax_temp=1.0, **kwargs):
super().__init__(*args, **kwargs)
self.softmax_temp = softmax_temp
self.action_space = gym.spaces.Box(low=-np.inf, high=np.inf, shape=(13,), dtype=np.float32)
def step(self, action_vec):
# action_vec: logits over 12 experts + HOLD
logits = np.asarray(action_vec, dtype=np.float32) / max(1e-6, self.softmax_temp)
p = np.exp(logits - logits.max()) # softmax
p = p / (p.sum() + 1e-12)
t = self.dates_t[self._i]; tp1 = self.dates_tp1[self._i]
# Build convex combo target
w_target = pd.Series(0.0, index=self.tickers)
for k, name in enumerate(EXPERT_NAMES): # 0..11
w_target += p[k] * self.experts_weights[name].loc[t].reindex(self.tickers).fillna(0.0)
w_target += p[12] * self._w_prev.reindex(self.tickers).fillna(0.0)
# Execute with turnover cap & compute reward (same as base env) ...
# (reuse parent logic for turnover, costs, hold_bonus if desired)
...
Run it:
cfg = AblationCfg(name="softmix_tau_0.7", policy_type="softmix", softmax_temp=0.7)
res_soft = run_ablation(cfg)
What to watch:
- Often lower turnover for similar returns; sometimes slightly better tails.
- If performance is the same as discrete, prefer discrete for interpretability.
10.7 Turnover Cap & Cost Sweeps
Question: How sensitive is behavior to caps and costs?
caps = [0.10, 0.15, 0.20, 0.30]
costs = [2.0, 5.0, 10.0]
rows = []
for cap in caps:
for c in costs:
cfg = AblationCfg(name=f"cap{int(cap*100)}_cost{int(c)}", turnover_cap=cap, trade_cost_bps=c)
rows.append(run_ablation(cfg))
sweep_tbl = pd.DataFrame(rows)
Interpretation:
- Lower caps & higher costs → lower turnover, often better CVaR, sometimes worse AnnRet.
- Pick a capacity-aware point (e.g., cap 15–20%, 5 bps) if you intend to trade size.
10.8 Walk-Forward & Reverse-Time
Walk-Forward: Roll yearly windows: train up to year $Y$, validate on $Y+1$, test on $Y+2$. Aggregate OOS. Reverse-Time: Train on late years, test on early years to see if the method relies on recent quirks.
Implement as loops slicing
weekly_retsandexperts_weightsby date; reuse the same train/validate code. Aggregate metrics and compare to the fixed-split results.
10.9 Entropy & Clip Sensitivity
Question: Are results brittle to PPO knobs?
grid = list(itertools.product([0.003, 0.005, 0.01], [0.2, 0.3, 0.4]))
rows = []
for ent, clip in grid:
cfg = AblationCfg(name=f"ent{ent}_clip{clip}", ent_coef=ent, clip_range=clip)
rows.append(run_ablation(cfg))
sens_tbl = pd.DataFrame(rows)
Interpretation:
- Too low
ent_coef→ premature collapse (one expert). - Too high
clip_range→ unstable updates. - Pick a flat region (robustness).
10.10 Seed Robustness
Run 3–5 seeds for the baseline config and key ablations:
def multi_seed(cfg_base, seeds=(17, 42, 123, 777, 1001)):
rows = []
for s in seeds:
cfg = AblationCfg(**{**asdict(cfg_base), "seed": s})
rows.append(run_ablation(cfg))
df = pd.DataFrame(rows)
return df.describe()[["AnnRet","Sharpe","CVaR5","MaxDD","Turnover"]]
print(multi_seed(AblationCfg(name="base")))
print(multi_seed(AblationCfg(name="dd_0.02", dd_penalty_lambda=0.02)))
Interpretation: Small variance across seeds is a good sign; large spread hints at insufficient signal or too-aggressive PPO.
10.11 Expert Pool Variants
Remove families/lookbacks to test redundancy:
- Only HRP vs Only HERC
- No long lookbacks (≤252d) vs No short lookbacks (≥504d)
Rebuild the experts registry for each variant and re-run the base training/eval.
What to watch:
- If results barely change, your pool has redundancy (good for stability).
- If performance collapses, a particular subset carries most value — document it.
10.12 Diagnostics you should always run
- Leakage Sentinel: Intentionally shift weekly returns by +1 week in evaluation; Sharpe should collapse. If not, you have indexing leakage.
- Cap-Hit Rate: % of weeks where turnover ≈ cap. High values mean the policy wants to move faster — consider lowering cap or increasing κ.
- Action Usage Bars: Count each action (including HOLD). If one expert dominates 80%+ of weeks, check entropy, features, and whether the pool is too narrow.
- Equity Attribution: Multiply weights by next-week returns by sleeve (Equity/Duration/Credit/Real Assets) to see where P&L comes from.
- Policy Entropy Over Time: Plot policy entropy by week during OOS; sudden drops may indicate overconfidence.
- Stress vs Non-Stress Summary: As in Section 9 — PPO should HOLD more and lose less in stress.
10.13 Reporting template (table)
Use a compact table to compare ablations to the Base config:
| Config | AnnRet | Sharpe | Sortino | CVaR@5% | MaxDD | Turnover | CostDrag |
|-------------------|--------|--------|---------|---------|-------|----------|----------|
| Base (discrete) | | | | | | | |
| No Regime | | | | | | | |
| No HOLD Bonus | | | | | | | |
| +DD λ=0.02 | | | | | | | |
| SoftMix τ=0.7 | | | | | | | |
| Cap=15%, Cost=5bp | | | | | | | |
10.14 One-paragraph takeaway
Ablations separate essential from nice-to-have. In practice you’ll often find: regime cues and a tiny drawdown penalty help tails; the HOLD bonus is a small but useful nudge; SoftMix can reduce turnover but trades off interpretability; and sensible caps/costs matter more than another point of Sharpe. If results hold across seeds, costs, and splits, you’ve got something you can trust.
11. What Worked / What Didn’t
Let’s be candid. This section distills the engineering wins, the misses, and the lessons that actually saved time. Use it as a checklist when you adapt the template to your own data.
11.1 What worked (keep these)
-
Switching among robust experts (HRP/HERC) rather than learning raw weights. The agent makes low-dimensional, interpretable choices (“follow HERC-252d” or “HOLD”) and avoids the overfit traps of end-to-end allocation.
-
Weekly cadence with costs & caps baked into the environment. This single choice made behavior tradable: lower churn, realistic equity curves, and fewer “paper alpha” illusions.
-
Compact state features. Recent expert performance at 1/4/12 weeks + a handful of regime cues (vol, trends, stress) were enough. Bigger feature sets didn’t help.
-
HOLD option that actually does nothing. Combined with a turnover cap, HOLD becomes a first-class action. The agent used it in stress pockets, cutting tail risk without complex signals.
-
Tiny hyperparameter sweep. Selecting only the learning rate by validation Sharpe kept the work honest and the model reproducible.
-
Common execution wrapper for PPO and all baselines. Same caps, same costs, same turnover limit. This made comparisons apples-to-apples and killed a whole category of arguments.
11.2 What didn’t (or mattered less than expected)
-
Giant networks and fancy reward shaping. Weekly data gives you hundreds of decisions, not tens of thousands. Bigger nets just memorized noise. Small MLPs were enough.
-
Exotic regime features. Fancy macro composites and dozens of indicators were brittle. The simple stress rule (SPY↓ & IEF↑), coarse trend flags, and a vol proxy were more robust.
-
Over-optimizing PPO knobs. Hours of tuning
clip_range,gae_lambda,vf_coefseldom beat the default-ish, stable settings. When results were fragile, data/logic issues were the culprit. -
Baking turnover penalties into the expert construction. It blurred responsibilities. Better: keep experts “pure” and enforce turnover at the execution layer.
-
Measuring on gross returns. It made everything look better than it trades. Net-of-cost (and a reported cost drag) told the real story.
11.3 Biggest time-savers (do these early)
-
Index alignment tests. Assert that decisions at $t$ only use information up to $t$, and rewards use $t{+}1$ returns. A one-line sentinel (shifting returns by +1 to force performance to collapse) catches leakage instantly.
-
Parquet caches for weekly returns and expert weights. Training and ablations get 10× faster, and your experiments become repeatable.
-
One registry for experts. A dict
{expert_name: path}simplified loading, ablations, and logging. -
Shared metrics function. A single
metrics_from_run()(Sharpe, Sortino, CVaR@5, MaxDD, Turnover, CostDrag) prevented drift between notebooks and plots.
11.4 Surprises (and how we handled them)
-
Cap friction appears as “want-to-move” pressure. The agent often hit the turnover cap right after regime shifts. That’s informative: it wanted to rotate, but we throttled it for tradability. Solution: accept it (by design), or slightly lower entropy to reduce thrash.
-
HOLD bonus works best when tiny. Too big and the agent hides in cash; too small and it’s irrelevant. A small nudge (e.g., 0.0005 per stress week) was the sweet spot.
-
Soft mixture-of-experts reduced turnover but blurred narrative. Nice for smoother trading; less nice for storytelling (“we were 37% HRP-120 + 21% HERC-504…”). We kept discrete as the mainline and used SoftMix as an ablation.
11.5 Practical tips for readers porting this
-
Match frequency and costs to your venue. If you switch to daily cadence, rescale lookbacks (in days, not weeks) and cost assumptions (5–10 bps may be more realistic).
-
Respect inception dates. Do not forward-fill pre-inception returns. Drop that asset in that window or force its weight to zero before normalization.
-
Constrain first, optimize second. Set realistic per-asset caps and turnover caps up front. Then train PPO. You’ll waste fewer cycles on untradeable behavior.
-
Prefer conservative covariance/cluster settings. For HRP/HERC, robust covariances (e.g., Ledoit-Wolf) and simple linkages (ward) were stable defaults.
-
Seed and version-pin everything. You’ll thank yourself later when someone asks, “Can you reproduce the 2019 validation Sharpe?”
11.6 Pitfalls & quick fixes
| Pitfall | Symptom | Quick Fix |
|---|---|---|
| Leakage via misaligned indices | Validation/OOS Sharpe suspiciously high | Shift returns by +1 as a sentinel; ensure t → t+1 mapping everywhere |
| Policy collapses to one expert too early | Low entropy, choppy equity | Slightly increase ent_coef (e.g., 0.005 → 0.008); check reward scale |
| Excessive flip-flop | High turnover near cap every week | Increase kappa or lower turnover cap to 15%; consider SoftMix with low temperature |
| Best Expert beats PPO by a lot | Switching not adding value | Revisit state features and HOLD semantics; ensure validation LR selection is working |
| Beautiful backtest, bad tails | CVaR/MaxDD poor | Add a tiny drawdown penalty or tighten caps; verify stress/HOLD logic |
| Inconsistent metrics across scripts | Confusing reports | Centralize metrics in one function and reuse everywhere |
11.7 Myth vs reality (for RL in portfolios)
-
Myth: “RL will discover magical allocations.” Reality: RL shines at sequencing—here, timing robust experts and knowing when to do nothing.
-
Myth: “More features → better performance.” Reality: With weekly data, less is more. Focus on clean, causal signals.
-
Myth: “The cost model is just detail.” Reality: Costs and caps shape the learned behavior; get them wrong, and you train the wrong policy.
11.8 Decision checklist (before you hit ‘publish’)
- Are costs and caps identical across PPO and baselines?
- Do your plots use net-of-cost returns?
- Does a leakage sentinel collapse performance as expected?
- Does the agent HOLD more in stress weeks?
- Do you report Sortino, CVaR@5%, and MaxDD alongside Sharpe?
- Can you reproduce results from a clean run (pinned versions + seed)?
11.9 One-paragraph takeaway
The biggest win wasn’t a clever trick—it was discipline: robust experts, a tiny and interpretable action space, honest costs and caps, and minimal hyperparameter twiddling. The method’s edge comes from when not to trade as much as from what to hold. Keep it simple, prove there’s no leakage, and measure tails and turnover with the same rigor as returns.
12. Limitations, Risks, and Ethics
This section is here to keep us honest. It lists what this approach doesn’t cover, where it can fail, and the guardrails you should keep if you ever think about running it live. It also spells out ethics and compliance basics.
12.1 Modeling limits (what this method cannot promise)
- Weekly cadence ≠ intraday control. The agent reacts once per week; shocks inside the week are unmodeled.
- Finite history, finite decisions. You have hundreds of decisions, not tens of thousands—big models will overfit.
- Stationarity is fragile. HRP/HERC stability helps, but regime structure can still change (new asset behaviors, liquidity).
- Discrete expert set. The policy only chooses among predefined experts (+ HOLD). If the true optimal weight is outside that span, it can’t be reached in one step.
- Simple stress rule. Our stress flag is intentionally coarse. It won’t catch all bad weeks or all kinds of crises.
12.2 Data & evaluation risks
- Survivorship bias. If you used ETFs that didn’t exist early on without handling inception gaps correctly, results can look too good.
- Corporate actions & dividends. Using anything but adjusted closes will distort returns.
- Leakage via resampling. Mixing daily features with weekly rewards requires careful index alignment; off-by-one errors inflate performance.
- Validation creep. Repeatedly tweaking hyperparameters using a single validation year can silently overfit that year.
Mitigation: lock splits before experiments; run leakage sentinels (Section 10); add walk-forward and reverse-time checks.
12.3 Trading realism gaps
- Cost model simplicity. Using a constant bps ignores size, venue, and market impact; actual slippage can be nonlinear.
- Capacity limits. ETFs are liquid, but size matters. Turnover × AUM determines impact; our cap/penalty is only a proxy.
- Execution drift. Real trades rarely fill exactly at close; fills can drift, and cash residuals can differ.
- Tax & compliance. After-cost returns are not after-tax; some venues restrict rebalancing frequency or exposures.
Mitigation: stress-test at 5–10 bps, tighten turnover caps, simulate partial fills, and document trading windows.
12.4 Method-specific failure modes
- Cap pressure after regime flips. When trends flip, the agent may hit the turnover cap for several weeks—performance can lag.
- Over-reliance on one expert. If entropy is too low or features are uninformative, policy can collapse to a single expert.
- False comfort from HOLD. If stress detection is poor, the agent may HOLD at the wrong times, missing recoveries.
- SoftMix ambiguity (if used). Mixtures can reduce turnover but make behavior harder to interpret (and harder to debug).
Mitigation: monitor cap-hit rate, action diversity, and HOLD usage by regime; consider a tiny drawdown penalty for tail control.
12.5 Statistical fragility
- Multiple testing. Many ablations + choices = higher odds of spurious “wins.”
- Optimism from lucky periods. A good OOS period can still be luck. Different windows may show different rankings.
- Heavy tails & serial correlation. Standard errors/Sharpe assumptions can be over-optimistic for financial returns.
Mitigation: report confidence bands (e.g., block bootstrap); show per-year metrics; run multi-seed training.
12.6 Deployment risks (if you ever go live)
- Model drift. Distribution shift means past relationships can fade.
- Operational errors. Bad clocks, missing data, or broken caches lead to wrong trades.
- Vendor dependencies. Changes in APIs (prices, splits) can break pipelines without notice.
Mitigation:
- Add SLOs: data latency, completeness checks, “no-trade if missing X% data.”
- Kill switches: max daily drawdown, max turnover breach, missing-data halt.
- Shadow mode: run paper trades alongside baseline(s) before capital.
- Two-person rule for config changes; versioned deployment manifests.
12.7 Risk controls to keep (minimum viable governance)
- Position limits: per-asset, per-sleeve, aggregate risk budgets.
- Turnover limits: as enforced here; consider stricter in live trading.
- Exposure checks: no unintended leverage or short exposure if you expand beyond long-only.
- Pre-trade validation: sanity-check weights sum, caps, and data freshness.
- Post-trade reconciliation: compare intended vs. filled weights; quantify slippage.
- Monitoring dashboards: equity, drawdown, turnover, cap-hit%, action usage, cost drag, and stress-week performance.
12.8 Ethics & communication
- No overpromising. This is a template for research, not a guarantee of profit.
- Transparency. Publish net-of-cost results, show tails (CVaR/MaxDD), and disclose assumptions (costs, caps, data).
- Fair access. Avoid implying that readers can replicate live results without capacity/cost considerations.
- Privacy & data rights. If you add alt-data later, ensure you have the legal right to use and redistribute it.
- Compute footprint. Weekly PPO is light, but still consider energy use if you scale up; prefer smaller models.
Plain disclaimer: This content is for educational purposes only and is not investment advice. Past performance, backtested or otherwise, is not indicative of future results.
13. Reproducibility
This section gives you a copy-paste playbook so anyone (including future-you) can reproduce the results bit-for-bit: exact environments, seeds, cached data, folder structure, one-click runs, and lightweight tests.
13.1 Principles (why this works)
- Pin everything (packages + data snapshot).
- Cache deterministically (Parquet files with fixed index).
- One source of truth (a
config.yamlyou pass everywhere). - Single commands for train → validate → test.
- Checks (hashes + simple tests) after each step.
13.2 Folder layout (copy this)
.
├─ config/
│ ├─ config.yaml # dates, costs, caps, seed, paths
│ └─ ablations.yaml # optional: named configs for Section 10
├─ data/
│ ├─ weekly_prices.parquet # cached snapshot (W-FRI Adj Close)
│ ├─ weekly_returns.parquet # cached weekly returns
│ └─ _HASH.txt # SHA256 of both files + tickers list
├─ experts_cache/
│ ├─ hrp_60d.parquet
│ ├─ herc_60d.parquet
│ └─ ... (one per expert)
├─ models/
│ ├─ ppo_best.zip
│ └─ checkpoints/ # per-LR saves (optional)
├─ outputs/
│ ├─ figures/
│ └─ csv/
├─ scripts/
│ ├─ 00_build_data.py
│ ├─ 01_build_experts.py
│ ├─ 02_train_select.py
│ ├─ 03_eval_oos.py
│ └─ 99_utils.py
├─ tests/
│ ├─ test_alignment.py
│ ├─ test_metrics.py
│ └─ test_env_sanity.py
├─ requirements.txt
├─ environment.yml # optional conda env
├─ Makefile
└─ README.md
13.3 Config (single source of truth)
# config/config.yaml
seed: 42
universe: [SPY, IEFA, EEM, IEI, IEF, TLT, LQD, HYG, GLD, DBC]
dates:
start: "2005-01-01"
end: "2025-09-01"
splits:
train: ["2010-01-01","2018-12-31"]
valid: ["2019-01-01","2019-12-31"]
oos: ["2020-01-01","2025-09-01"]
frequency: "W-FRI"
costs:
trade_cost_bps: 2.0
kappa_turnover: 0.002
hold_bonus: 0.0005
constraints:
max_per_asset: 0.35
turnover_cap: 0.20
cash_allowed: true
max_cash: 0.05
experts:
lookbacks_days: [60,120,252,504,756,1008]
models: ["HRP","HERC"]
ppo:
net_arch: {pi: [1024,512], vf: [1024,512]}
gamma: 0.99
gae_lambda: 0.95
ent_coef: 0.005
clip_range: 0.30
target_kl: 0.20
batch_size: 256
n_steps: 2048
total_timesteps: 400000
lr_grid: [1e-4, 3e-4, 1e-3]
paths:
data_dir: "data"
experts_dir: "experts_cache"
models_dir: "models"
outputs_dir: "outputs"
Keep all hard numbers here. Scripts should read only this file.
13.4 Environment (pin packages)
Option A — requirements.txt (pip)
numpy==1.26.4
pandas==2.2.2
matplotlib==3.8.4
yfinance==0.2.40
pyarrow==16.1.0
riskfolio-lib==4.1.0
gymnasium==0.29.1
stable-baselines3==2.3.2
shimmy==1.3.0
torch==2.2.2
Install:
python -m venv .venv && source .venv/bin/activate
pip install -r requirements.txt
python -c "import torch, numpy, pandas; print('OK')"
Option B — Conda (more reproducible)
# environment.yml
name: rl-portfolio
channels: [conda-forge, pytorch]
dependencies:
- python=3.11
- numpy=1.26
- pandas=2.2
- matplotlib=3.8
- pyarrow=16.1
- pip
- pip:
- yfinance==0.2.40
- riskfolio-lib==4.1.0
- gymnasium==0.29.1
- stable-baselines3==2.3.2
- shimmy==1.3.0
- torch==2.2.2
Create & activate:
conda env create -f environment.yml
conda activate rl-portfolio
13.5 Seeding (make RNGs deterministic)
Put this at the top of every entry script:
# scripts/99_utils.py
import os, random, numpy as np
def set_global_seed(seed: int):
os.environ["PYTHONHASHSEED"] = str(seed)
random.seed(seed)
np.random.seed(seed)
try:
import torch
torch.manual_seed(seed)
torch.use_deterministic_algorithms(False) # PPO uses CUDA ops that may not be fully deterministic
except Exception:
pass
Call set_global_seed(cfg["seed"]) in each script. Also pass seed=cfg["seed"] into PPO.
Note: Exact bit-for-bit equality across GPUs/CPUs isn’t guaranteed with PPO, but metrics should match within tiny tolerances given fixed data.
13.6 Step 1 — Build and cache data (deterministic)
# scripts/00_build_data.py
from pathlib import Path
import pandas as pd, yfinance as yf, hashlib, json
from 99_utils import set_global_seed
import yaml, numpy as np, sys
cfg = yaml.safe_load(open("config/config.yaml"))
set_global_seed(cfg["seed"])
tickers = cfg["universe"]
START, END = cfg["dates"]["start"], cfg["dates"]["end"]
data_dir = Path(cfg["paths"]["data_dir"]); data_dir.mkdir(exist_ok=True)
px = yf.download(tickers, start=START, end=END, auto_adjust=False, progress=False)["Adj Close"].sort_index()
weekly_px = px.resample(cfg["frequency"]).last()
weekly_rets = weekly_px.pct_change().dropna(how="all")
weekly_px.to_parquet(data_dir/"weekly_prices.parquet")
weekly_rets.to_parquet(data_dir/"weekly_returns.parquet")
# write hash file
h = hashlib.sha256()
for p in ["weekly_prices.parquet","weekly_returns.parquet"]:
h.update(open(data_dir/p, "rb").read())
h.update(",".join(tickers).encode())
(data_dir/"_HASH.txt").write_text(h.hexdigest())
print("Data cached. SHA256:", h.hexdigest())
Data determinism: Public APIs can revise history (rare). Commit
data/*.parquet+_HASH.txtinto your repo for fully reproducible runs.
13.7 Step 2 — Build expert caches
# scripts/01_build_experts.py
import yaml, pandas as pd
from pathlib import Path
from 99_utils import set_global_seed
from your_expert_module import build_expert_cache # Section 4 code factored here
cfg = yaml.safe_load(open("config/config.yaml"))
set_global_seed(cfg["seed"])
weekly_rets = pd.read_parquet(Path(cfg["paths"]["data_dir"])/"weekly_returns.parquet")
# If your experts use daily returns, also load daily Adj Close and compute daily returns here.
registry = build_expert_cache(
daily_px=pd.read_parquet(Path(cfg["paths"]["data_dir"])/"daily_prices.parquet") if (Path(cfg["paths"]["data_dir"])/"daily_prices.parquet").exists() else None,
weekly_rets=weekly_rets,
lookbacks_days=cfg["experts"]["lookbacks_days"],
out_dir=cfg["paths"]["experts_dir"]
)
print("Experts cached:", list(registry.keys()))
Save
registry.jsonif you like, mapping expert → path.
13.8 Step 3 — Train + select LR, save best model
# scripts/02_train_select.py
import yaml, pandas as pd, os, shutil
from stable_baselines3 import PPO
from 99_utils import set_global_seed
from env_meta import make_train_env, make_valid_env # Section 5 factored helpers
from eval_utils import eval_on_env # Section 7 helper
cfg = yaml.safe_load(open("config/config.yaml"))
set_global_seed(cfg["seed"])
train_env = make_train_env(cfg)
valid_env = make_valid_env(cfg)
best = None
for lr in cfg["ppo"]["lr_grid"]:
model = PPO("MlpPolicy", train_env,
learning_rate=lr,
n_steps=cfg["ppo"]["n_steps"],
batch_size=cfg["ppo"]["batch_size"],
gamma=cfg["ppo"]["gamma"],
gae_lambda=cfg["ppo"]["gae_lambda"],
ent_coef=cfg["ppo"]["ent_coef"],
clip_range=cfg["ppo"]["clip_range"],
target_kl=cfg["ppo"]["target_kl"],
seed=cfg["seed"],
policy_kwargs=dict(net_arch=dict(pi=cfg["ppo"]["net_arch"]["pi"],
vf=cfg["ppo"]["net_arch"]["vf"])))
model.learn(total_timesteps=cfg["ppo"]["total_timesteps"])
metrics = eval_on_env(model, valid_env)
path = f'models/ppo_lr{lr:.0e}.zip'
os.makedirs("models", exist_ok=True); model.save(path)
if (best is None) or (metrics["sharpe"] > best["sharpe"]):
best = dict(lr=lr, path=path, **metrics)
shutil.copyfile(best["path"], "models/ppo_best.zip")
print("Selected LR:", best["lr"], "Val Sharpe:", round(best["sharpe"],3))
13.9 Step 4 — Evaluate OOS and write artifacts
# scripts/03_eval_oos.py
import yaml, pandas as pd, json
from 99_utils import set_global_seed
from baselines import run_eqw, run_6040, run_best_expert, run_random # Section 8 wrappers
from ppo_rollout import run_ppo_oos # deterministic rollout
cfg = yaml.safe_load(open("config/config.yaml"))
set_global_seed(cfg["seed"])
ppo_run = run_ppo_oos(cfg, "models/ppo_best.zip")
eqw_run = run_eqw(cfg)
b6040_run= run_6040(cfg)
best_run = run_best_expert(cfg) # chosen on validation split
rnd_run = run_random(cfg, seed=cfg["seed"])
from metrics import metrics_from_run
rows = [
("PPO Switcher", metrics_from_run(ppo_run)),
("Equal Weight", metrics_from_run(eqw_run)),
("60/40", metrics_from_run(b6040_run)),
("Best Expert", metrics_from_run(best_run)),
("Random", metrics_from_run(rnd_run)),
]
tbl = pd.DataFrame({k:v for k,v in rows}).T
outdir = cfg["paths"]["outputs_dir"]; os.makedirs(f"{outdir}/csv", exist_ok=True)
tbl.to_csv(f"{outdir}/csv/oos_summary.csv", float_format="%.6f")
print(tbl)
Also save plots to outputs/figures/ (Section 9 code).
13.10 Makefile (single-command runs)
.PHONY: data experts train eval all clean
data:
\tpython scripts/00_build_data.py
experts: data
\tpython scripts/01_build_experts.py
train: experts
\tpython scripts/02_train_select.py
eval: train
\tpython scripts/03_eval_oos.py
all: data experts train eval
clean:
\trm -rf models outputs experts_cache
Run everything:
make all
13.11 One-click Colab
At the top of your notebook:
[Open in Colab](https://colab.research.google.com/github/<your-repo>/blob/main/notebooks/colab.ipynb)
In the Colab notebook:
!pip install -r requirements.txt!python scripts/00_build_data.py!python scripts/01_build_experts.py!python scripts/02_train_select.py!python scripts/03_eval_oos.py
Colab tips: set
TORCH_USE_CUDA_DSA=0, use CPU or T4; SB3 runs fine at weekly cadence.
13.12 Lightweight tests (fast, critical)
# tests/test_alignment.py
import pandas as pd
def test_no_lookahead(weekly_rets):
idx = weekly_rets.index
assert (idx[1:] > idx[:-1]).all()
# tests/test_env_sanity.py
def test_step_advances(env):
obs, info = env.reset()
obs2, r, done, trunc, info = env.step(env.action_space.sample())
assert info["date"] > env.dates_t[0]
# tests/test_metrics.py
from metrics import metrics_from_run
def test_metrics_shapes(run_eqw):
m = metrics_from_run(run_eqw)
for k in ["AnnRet","Sharpe","Sortino","CVaR5","MaxDD","Turnover","CostDrag"]:
assert k in m
Run:
pytest -q
13.13 Hashes & metadata (artifact labels)
- Write a small
outputs/manifest.json:
{
"seed": 42,
"data_hash": "SHA256_OF_DATA",
"config_hash": "SHA1_OF_CONFIG",
"model": "models/ppo_best.zip",
"train_dates": ["2010-01-01","2018-12-31"],
"valid_dates": ["2019-01-01","2019-12-31"],
"oos_dates": ["2020-01-01","2025-09-01"],
"package_versions": "pip freeze output here"
}
- Capture
pip freeze > outputs/pip_freeze.txtafter install.
13.14 Determinism caveats (be realistic)
- Market data can get small historical fixes. Keep Parquet snapshots in-repo or in a data bucket.
- GPU vs CPU may yield tiny numerical diffs; judge reproducibility by metrics, not byte-identical trajectories.
- OS/BLAS differences can change clustering at the 1e-12 level; robust covariances (e.g., Ledoit-Wolf) minimize this.
13.15 Quick start (the three commands)
# 1) install
pip install -r requirements.txt
# 2) build everything
make all
# 3) open results
cat outputs/csv/oos_summary.csv
13.16 What to remember
- Pin packages; snapshot data; seed RNGs.
- Drive every script from config.yaml.
- Use a Makefile (or
tox/nox) to wire steps. - Add tiny tests for alignment and metrics.
- Save artifacts + metadata so results are auditable.
14. FAQs
Quick, practical answers to the questions readers ask most. Skim the headings and dive where needed.
Basics
Q1. Why “switch among experts” instead of learning raw portfolio weights? Because picking one of ~12 sensible, precomputed portfolios is a low-dimensional, interpretable decision that avoids overfitting. Weekly data gives you hundreds of decisions; end-to-end weight learning is high-variance and hard to trust.
Q2. Why PPO? Why a discrete policy? PPO gives stable updates (clip + KL), works well with noisy rewards, and has mature implementations. A discrete action set (“HRP-252d”, “HERC-504d”, “HOLD”) keeps learning stable and explanations human-readable.
Q3. What exactly does HOLD do? True do-nothing: it keeps last week’s executed weights. There’s no rebalancing to a target, so turnover≈0 (except tiny numerical drift).
Q4. Why weekly cadence? It’s tradable for most readers, reduces churn and leakage risk, and makes cause→effect clear. You still compute HRP/HERC on daily windows for better covariance estimates.
Design choices
Q5. Why HRP/HERC instead of Markowitz or IVP? HRP/HERC diversify without inverting a noisy covariance matrix, making them more stable in limited data. We still keep IVP as a safe fallback.
Q6. Why multiple lookbacks? Which ones matter most? Short windows adapt; long windows stabilize. The mix gives the agent options. In many markets, mid/long windows (e.g., 252–504d) anchor behavior; short (60–120d) help in fresh trends.
Q7. Why cap turnover at 20% and per-asset at 35%? They are guardrails for capacity and realism. Lower caps → smoother, slower; higher caps → faster but costlier. Keep them constant across PPO and baselines for fair comparisons.
Q8. What’s the point of the extra turnover penalty if we already pay costs? Costs model reality; the penalty shapes behavior to prefer smaller moves even when costs are low or mis-specified. Together they yield calmer, more tradable policies.
Q9. Why include a HOLD bonus under stress? Isn’t that cheating? It’s a tiny nudge (not a rule) to reflect that “doing less” can be rational in risk-off shocks. You can ablate it; results should degrade gracefully, not collapse.
Implementation
Q10. How do I switch to daily decisions safely?
- Resample prices to D instead of W-FRI.
- Scale lookbacks sensibly (e.g., 252d still ~1Y).
- Increase costs (e.g., 5–10 bps).
- Expect more decisions → possibly smaller networks and a tad more entropy to prevent stickiness.
Q11. How do I add more experts (e.g., min-var, classic risk parity, momentum sleeves)? Add them to the expert cache (same interface: weights per date, long-only caps applied). More experts = richer choices, but also larger state (more performance features). Keep the state compact (e.g., still 1/4/12-week summaries).
Q12. Where do I apply the turnover cap—expert stage or execution? Execution. Experts output clean targets; the environment caps the move from last week to this week. This separation keeps logic clear.
Q13. Should I normalize/standardize observations? Mild winsorization/standardization can help PPO stability. Save the scaler and reuse it unchanged at validation/OOS.
Q14. How big should the network be? Small. Two layers (e.g., 1024→512) are plenty at weekly cadence. Bigger nets overfit quickly with limited decisions.
Q15. Do I need reward normalization? Usually no. Rewards are already in return space (bps). If learning is unstable, consider advantage normalization (PPO does this internally) before altering reward scale.
Evaluation & reliability
Q16. How do I check for leakage in one minute?
Run a sentinel: shift weekly_rets by +1 week in evaluation. If Sharpe doesn’t crater, you’ve got leakage.
Q17. Are your metrics annualized correctly for weekly data? Yes—use A=52.
- Sharpe/Sortino: multiply mean by
A, divide stdev by√A. - Ann. return: compound equity to end, raise to
A / n.
Q18. Why report CVaR@5% and MaxDD? They capture tail risk and path risk. A strategy with a slightly lower Sharpe but much better CVaR/MaxDD is often preferable.
Q19. Why did Best Single Expert beat PPO in my run? Possible causes: weak features, insufficient exploration (low entropy), or a too-rich expert set where one dominates. Check action usage, cap-hit rate, and try a small drawdown penalty.
Q20. How many seeds should I try? 3–5 seeds for the base config and any important ablation. Report mean ± stdev for Sharpe, CVaR, MaxDD, and Turnover.
Data concerns
Q21. How do I avoid survivorship bias with ETFs? Handle inception dates: drop assets from windows where they lack data (or force weight=0). Never forward-fill pre-inception returns.
Q22. Which price field should I use? Adjusted Close (dividends/splits). Using raw Close understates returns for dividend-paying funds.
Q23. Should I snapshot data? Yes. Cache to Parquet and store a hash. APIs can occasionally revise history.
Extensions
Q24. Can I allow leverage or shorts? You can, but then you must model financing/borrow costs and expand your risk controls. This tutorial is long-only by design to keep things robust and reader-friendly.
Q25. Can I run this on crypto or single stocks? Yes—replace the tickers and refit costs/caps. Beware 24/7 trading (for crypto), different volatility, and higher slippage.
Q26. How do I add a soft mixture-of-experts head? Output a probability vector over experts + HOLD (softmax), blend their targets, then apply the same turnover cap. Keep the rest identical so comparisons are fair.
Q27. Walk-forward vs fixed splits—what should I publish? Publish both if possible. Fixed split is easier to read; walk-forward better reflects deployment and reduces “lucky window” risk.
Troubleshooting
Q28. Policy collapses to one expert on step 1—help.
Raise ent_coef slightly (e.g., 0.005→0.008), lower clip_range (0.3→0.2), or reduce LR. Verify features are scaled and informative.
Q29. Turnover is constantly at the cap.
Increase kappa_turnover, reduce turnover_cap (15%), or try SoftMix with a slightly lower temperature to glide instead of jump.
Q30. Beautiful equity curve, ugly tails. Add a tiny drawdown penalty (e.g., λ=0.02), double-check stress/HOLD logic, and ensure your equity/MaxDD are computed on net-of-cost returns.
Q31. Validation Sharpe looks amazing, OOS meh. Classic over-tuning. Shrink the sweep (often just learning rate), use walk-forward, and simplify features.
Q32. Results differ run-to-run. Set seeds everywhere, pin package versions, snapshot data, and prefer CPU for bit-stability. Expect tiny diffs; judge by metrics, not identical trajectories.
Copy-paste snippets
Leakage sentinel (evaluation only):
leaky_rets = weekly_rets.shift(-1) # WRONG ON PURPOSE
# Re-run evaluation with leaky_rets; Sharpe should crash if your pipeline was honest.
Downside stdev (Sortino):
downside = np.sqrt(np.mean(np.minimum(0, r)**2))
sortino = (r.mean()*52) / (downside*np.sqrt(52) + 1e-12)
Max Drawdown from net returns:
eq = (1 + r).cumprod()
dd = 1 - eq/eq.cummax()
maxdd = dd.max()
Final — Results Visual
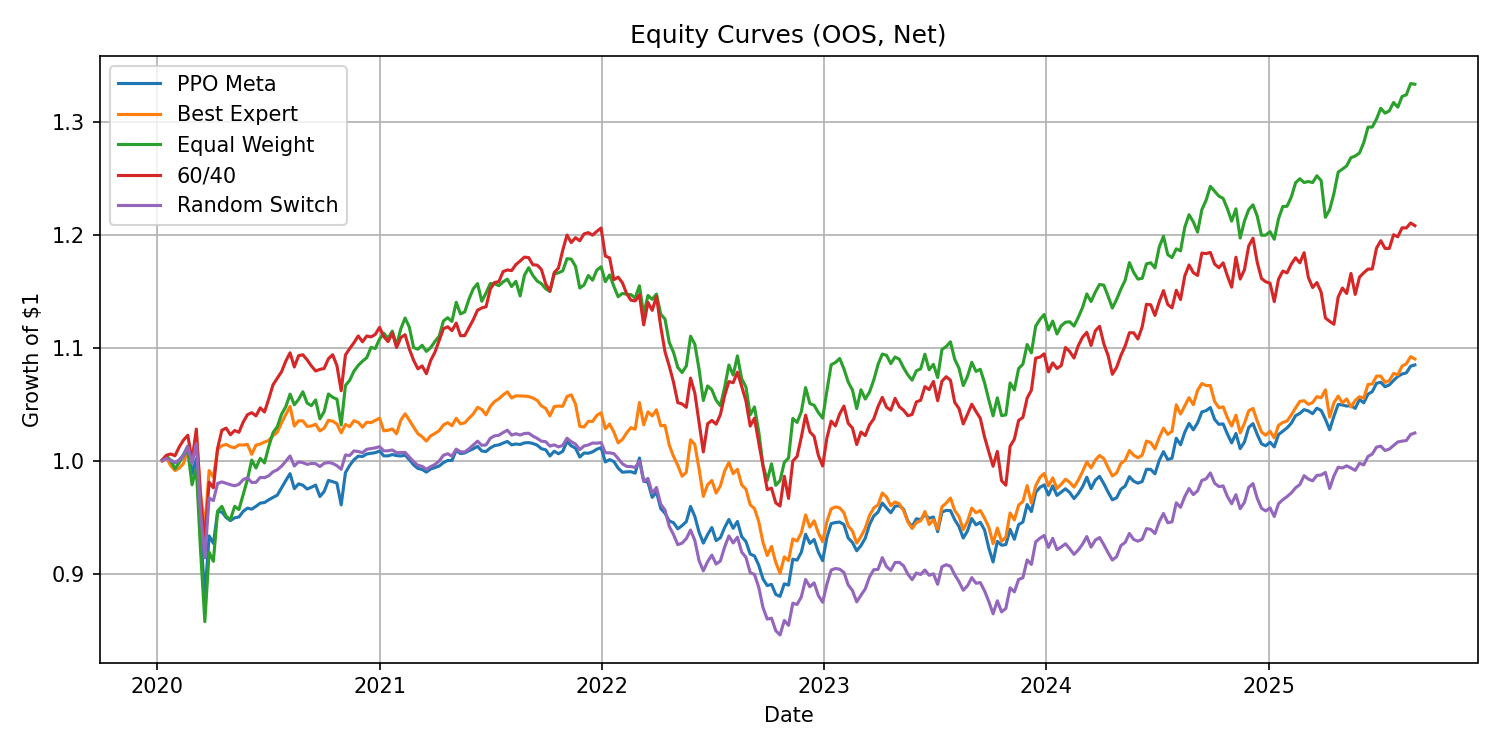
This figure is the main results visualization: it shows the growth of $1 (2020–2025) after trading costs, comparing the PPO meta-controller against baselines (Best Expert, Equal Weight, 60/40, Random Switch). All strategies were evaluated with the same constraints and turnover cap, so the comparison is fair and tradable.