Introduction
This paper studies the problem of zero-shot generalization in reinforcement learning and introduces an algorithm that trains an ensamble of maximum reward seeking agents and an maximum entropy agent. At test time, either the ensemble agrees on an action, and we generalize well, or we take exploratory actions with the help of maximum entropy agent and drive us to a novel part of the state space, where the ensemble may potentially agree again. This method combined with an invariance based approach achieves new state-of-the-art results on ProcGen.
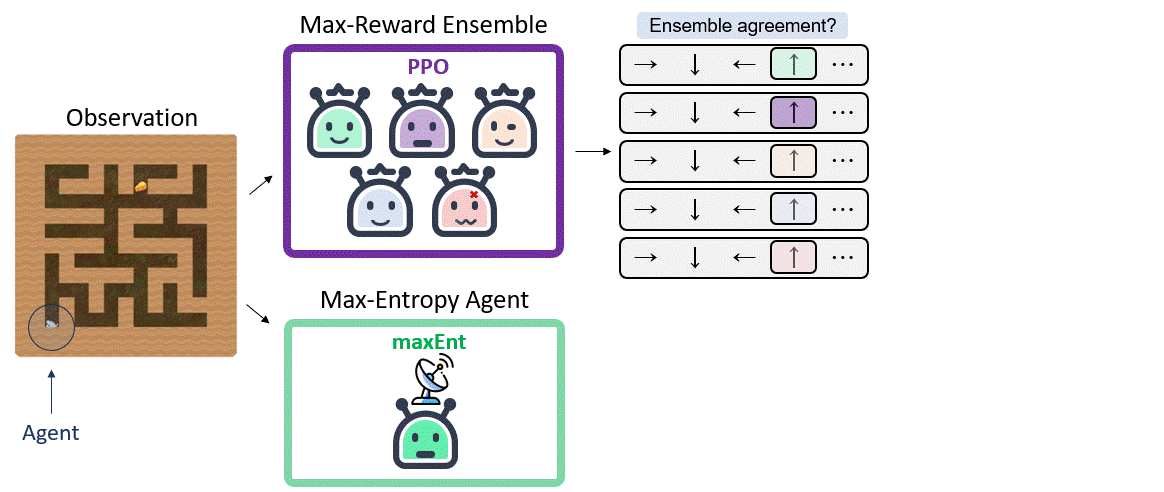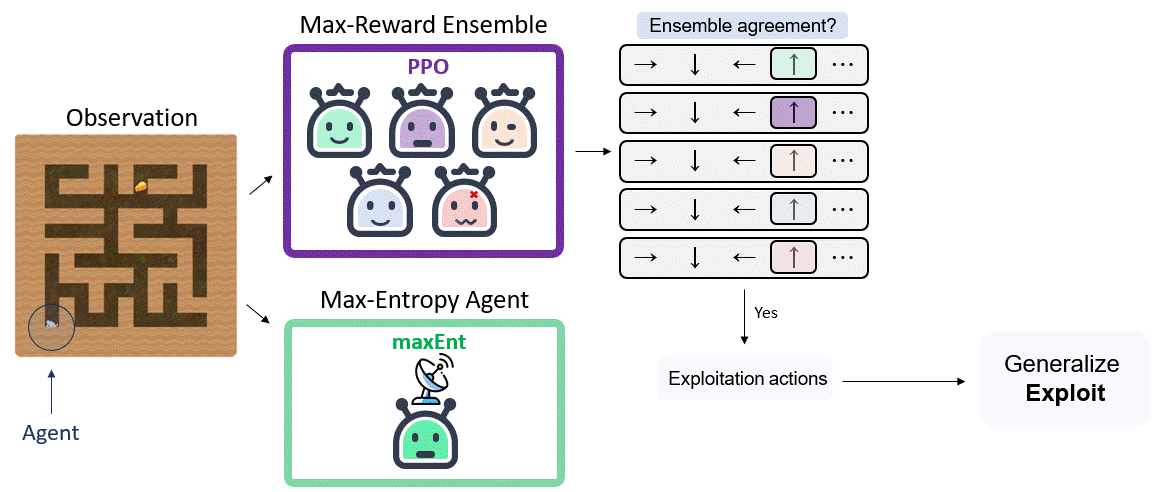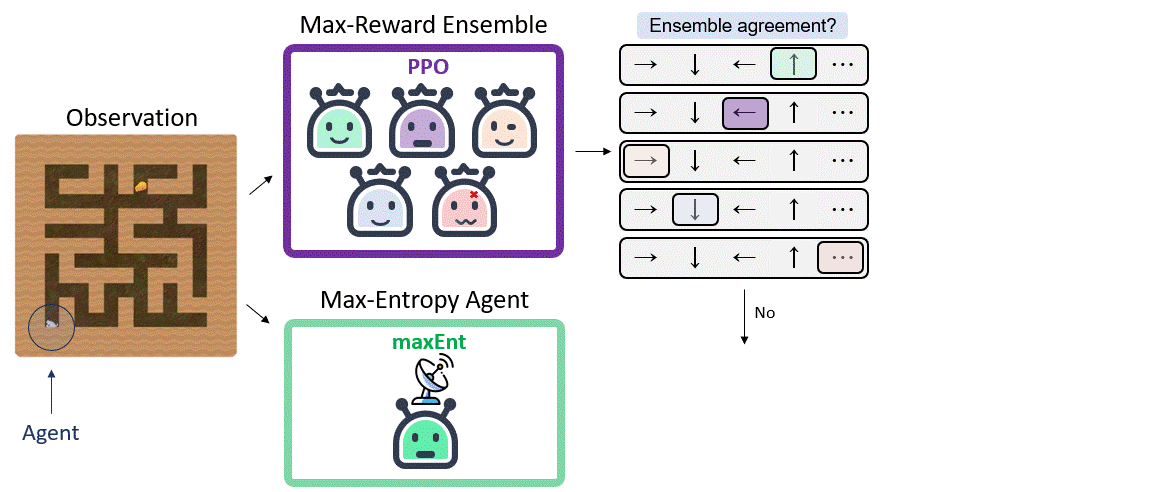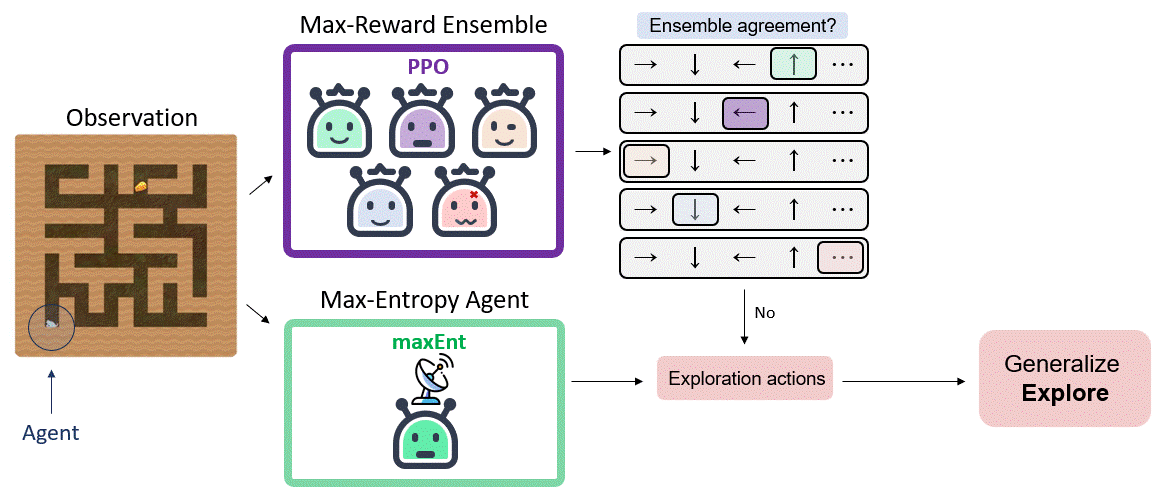
Background
I know it’s a lot to take in! You may be wondering:
- What is reinforcement learning? 🥺
- What generalization means for RL? 🥲
- What is zero-shot generalization? 🥹
- What are max reward and max entropy agents?! ☹️
- What is an ensamble of them?!! 😟
- What is an invariance based approach? 😓
- And what the heck is ProcGen?!!! 😠
Don’t worry! We are going to cover all of that and more! And you are going to fully understand this paper and finish reading this article with an smile 🙂!
What is reinforcement learning?
Reinforcement learning is learning what to do—how to map situations to actions—so as to maximize a numerical reward signal. Imagine yourself right now, in reinforcement learning terms, you are an agent and everything that is not you, is your environment. You perceive the world through your senses (e.g., eyes, ears, etc.) and what you perceive turns into electrical signals that your brain processes to form an understanding of your surroundings (state). Based on this understanding, you make decisions (actions) with the goal of achieving the best possible outcome for yourself (reward).

In a more formal sense, reinforcement learning involves the following components:
- Agent: The learner or decision maker (e.g., you).
- Environment: Everything the agent interacts with (e.g., the world around you).
- State ($s$): A representation of the current situation of the agent within the environment (e.g., what you see, hear, and feel at any given moment).
- Actions ($a$): The set of all possible moves the agent can make (e.g., moving your hand, walking, speaking).
- Reward ($r$): The feedback received from the environment in response to the agent’s action (e.g., pleasure from eating food, pain from touching a hot surface).
- Policy ($\pi$): A strategy used by the agent to decide which actions to take based on the current state (e.g., your habits and decision-making processes).
- Value Function ($V$): A function that estimates the expected cumulative reward of being in a certain state and following a particular policy (e.g., your prediction of future happiness based on current actions).
The objective of the agent is to develop a policy that maximizes the total cumulative reward over time. This is typically achieved through a process of exploration (trying out new actions to discover their effects) and exploitation (using known actions that yield high rewards).
In mathematical terms, the goal is to find a policy $\pi$ that maximizes the expected return $G_t$, which is the cumulative sum of discounted rewards:
$$ G_t = r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \cdots $$
where $\gamma$ (0 ≤ $\gamma$ < 1) is the discount factor that determines the importance of future rewards.
For a more thorough and in depth explanation of reinforcement learning please refer to Lilian Weng excelent blog post A (Long) Peek into Reinforcement Learning.
What generalization means for RL?
In reinforcement learning, generalization involves an agent’s ability to apply learned policies or value functions to new states or environments that it has not encountered during training. This is essential because it is often impractical or impossible to train an agent on every possible state it might encounter.
There are bunch of methods that researchers have used to tackle the problem of generalization in reinforcement learning that are summarized in the following diagram.

This paper focuses on RL-Specific solutions and specifically exploration technique to tackle the problem of generalization. If you’re interested to learn more about the generalization problem in reinforcement learning please refer to reference [3].
What is zero-shot generalization?
Zero-shot generalization in RL refers to the ability of an agent to perform well in entirely new environments or tasks without any prior specific training or fine-tuning on those environments or tasks. This is a significant challenge because it requires the agent to leverage its learned representations and policies in a highly flexible and adaptive manner.
In order to define the objective of zero-shot generalization we first have to define what MDPs and POMDPs are.
Markov Decision Process (MDP):
MDP is a mathematical framework used to describe an environment in reinforcement learning where the outcome is partly random and partly under the control of a decision-maker (agent). A MDP is a tuple $M = (S, A, P_{init}, P, r, \gamma)$ where,
- States ($S \in \mathbb{R}^{|S|}$): A finite set of states that describe all possible situations in which the agent can be.
- Actions ($A \in \mathbb{R}^{|A|}$): A finite set of actions available to the agent.
- Initial State Distribution ($P_{init}$): A distribution of starting state $(s_0 \sim P_{init})$.
- Transition Probability ($P$): A function $P(s_{t+1}, s_t, a_t)$ representing the probability of transitioning from state $s_t$ to state $s_{t+1}$ after taking action $a_t$ $(s_{t+1} \sim P(.|s_t,a_t))$.
- Reward ($r: S \times A \rightarrow \mathbb{R}$): A function $r(s_t, a_t)$ representing the immediate reward $r_t$ received after transitioning from state $s_t$ due to action $a_t$ $(r_t = r(s_t, a_t))$.
- Discount Factor ($\gamma$): $(0 \leq \gamma < 1)$ is a constant that determines the importance of future rewards.
Partially Observable Markov Decision Process (POMDP):
POMDP extends MDPs to situations where the agent does not have complete information about the current state. Instead, the agent must make decisions based on partial observations. A POMDP is a tuple $M = (S, A, O, P_{init}, P, \Sigma, r, \gamma)$ where other that above definitions for MDP,
- Observation Space ($O$): A finite set of observations the agent can receive about the state.
- Observation Function ($\Sigma$): A function that given current state $s_t$ and current action $a_t$ gives us the current observation $o_t$ $(o_t = \Sigma(s_t, a_t) \in O)$.
If we set $O = S$ and $\Sigma(s,a) = s$, the POMDP turns into regular MDP.
Let the history at time $t$ be,
$$ h_t = \{ o_0, a_0, r_0, o_1, a_1, r_1, \dots, o_t \} $$
The agent’s next action is outlined by a policy $\pi$, which is a stochastic mapping from the history to an action probability,
$$ \pi(a|h_t) = P(a_t=a|h_t) $$
In this formulation, a history-dependent policy (and not a Markov policy) is required both due to partially observed states, epistemic uncertainty, and also for optimal maxEnt exploration.
We assume a prior distribution over POMDPs $P(M)$, defined over some space of POMDPs. For a given POMDP, an optimal policy maximizes the expected discounted return,
$$ \mathbb{E}_{\pi,M} \left[ \sum _{t=0}^{\infty} \gamma^t r(s_t,a_t) \right] $$
Where the expectation is taken over the policy $\pi(h_t)$, and the state transition probability $s_t \sim P$ of POMDP $M$.
Our generalization objective is to maximize the discounted cumulative reward taken in expectation over the POMDP prior,
$$ \mathcal{R}_ {pop}(\pi) = \mathbb{E}_ {M \sim P(M)} {\left[ \mathbb{E}_{\pi,M} {\left[ \sum _{t=0}^{\infty} \gamma^t r(s_t,a_t) \right]} \right]} $$
Seeking a policy that performs well in expectation over any POMDP from the prior corresponds to zero-shot generalization.
And as you may have guessed we don’t have access to true prior distribution of POMDPs so we have to estimate it with $N$ training POMDPs $M_1, M_2, \dots, M_N$ sampled from the true prior distribution $P(M)$. So we are going to maximize empirical discounted cumulative reward,
$$ \begin{align*} \mathcal{R}_ {emp}(\pi) &= \frac{1}{N} \sum _ {i=1}^{N} \mathbb{E} _ {\pi,M_i} \left[ \sum _ {t=0}^{\infty} \gamma^t r(s_t,a_t) \right] \\ &= \mathbb{E}_ {M \sim \hat{P}(M)} {\left[ \mathbb{E}_{\pi,M} {\left[ \sum _{t=0}^{\infty} \gamma^t r(s_t,a_t) \right]} \right]} \end{align*} $$
Where the empirical POMDP distribution $\hat{P}(M)$ can be different from the true distribution, i.e. $\hat{P}(M) \neq P(M)$. In general, a policy that optimizes the empirical reward may perform poorly on the population reward and this is known as overfitting in statistical learning theory.
What are max reward and max entropy agents?!
As we have seen, the goal of agents in reinforcement learning is to find a policy $\pi$ that maximizes the expected discounted return by focusing on actions that lead to the greatest immediate or future rewards. We call these common RL agents “max reward agents” in this paper. On the other hand, “max entropy agents” aim to maximize the entropy of the policy for visiting different states. Maximizing entropy encourages the agent to explore a wider range of actions that lead the agent to visit new states even when they don’t contribute any reward.
This type of agent will help us to make decisions when we have epistemic uncertainty about what to do at test time. Epistemic uncertainty basically means the uncertainty that we have because of our lack of knowledge and can be improved by gathering more information about the situation.
The insight of the authors of this paper is that learning a policy that effectively explores the domain is harder to memorize than a policy that maximizes reward for a specific task, and therefore they expect such learned behavior to generalize well.
What is an ensamble of them?!!
Ensembling in reinforcement learning involves combining the policies of multiple individual agents to make more accurate and robust decisions. The idea is that by aggregating the outputs of different agents, we can leverage their diverse perspectives and expertise to improve overall performance.
This paper uses an ensamble of max reward agents to help the agent decide on the overal epistemic uncetainty that we have at test time.
What is an invariance based approach?
Invariance based algorithms in reinforcement learning focus on developing policies that are robust to changes and variations in the environment. These algorithms aim to identify and leverage invariant features or patterns that remain consistent across different environments or tasks. The goal is to ensure that the learned policy performs well not just in the training environment but also in new, unseen environments.
This paper uses IDAAC algorithm which is a special kind of DAAC algorithm as its invariance based algorithm.
DAAC (Decoupled Advantage Actor-Critic) uses two separate networks, one for learning the policy and advantage, and one for learning the value. The value estimates are used to compute the advantage targets.
IDAAC (Invariant Decoupled Advantage Actor-Critic) adds an additional regularizer to the DAAC policy encoder to ensure that it does not contain episode-specific information. The encoder is trained adversarially with a discriminator so that it cannot classify which observation from a given pair $(s_i, s_j)$ was first in a trajectory.

For more information about IDAAC algorithm please refer to reference [4].
What the heck is ProcGen?!!!
Procgen is a benchmark suite for evaluating the generalization capabilities of reinforcement learning agents. It was developed by OpenAI and consists of a collection of procedurally generated environments that vary in terms of visual appearance, dynamics, and difficulty. The goal of Procgen is to provide a standardized and challenging set of environments that can be used to assess the ability of RL algorithms to generalize to unseen scenarios.

If you are new to reinforcement learning, I know these explanations are a lot to take in! If you find yourself lost, I recommend to check out the following courses at your leisure:
- Deep Reinforcement Learning (by Hugging Face 🤗)
- Reinforcement Learning (by Mutual Information)
- Introduction to Reinforcement Learning (by David Silver)
- Reinforcement Learning (by Michael Littman & Charles Isbell)
- Reinforcement Learning (by Emma Brunskill)
- Deep Reinforcement Learning Bootcamp 2017
- Foundations of Deep RL (by Pieter Abbeel)
- Deep Reinforcement Learning & Control (by Katerina Fragkiadaki)
- Deep Reinforcement Learning (by Sergey Levine)
After reviewing all this we can focus on the rest of the paper!
Hidden Maze Experiment
One of the key observation of the authors of this paper is that invariance is not enough for zero-shot generalization of reinforcemen learning algorithm. They designed the hidden maze experiment too demonstrate that. Imagine Maze, but with the walls and goal hidden in the observation. Arguably, this is the most task-invariant observation possible, such that a solution can still be obtained in a reasonable time.

An agent with memory can be trained to optimally solve all training tasks: figuring out wall positions by trying to move ahead and observing the resulting motion, and identifying based on its movement history in which training maze it is currently in. Obviously, such a strategy will not generalize to test mazes. Performance in Maze, where the strategy for solving any particular training task must be indicative of that task, has largely not improved by methods based on invariance
The following figure shows PPO performance on the hidden maze task, indicating severe overfitting.

As described by [5], an agent can overcome test-time errors in its policy by treating the perfect policy as an unobserved variable. The resulting decision making problem, termed the epistemic POMDP, may require some exploration at test time to resolve uncertainty. The article further proposed the LEEP algorithm based on this principle, which trains an ensemble of agents and essentially chooses randomly between the members when the ensemble does not agree, and was the first method to present substantial generalization improvement on Maze.
In this paper authors extend this idea and asked, How to improve exploration at test time?, and their approach is based on a novel discovery, when they train an agent to explore the training domains using a maximum entropy objective, they observe that the learned exploration behavior generalizes surprisingly well (much better than the generalization attained when training the agent to maximize reward).
In the following section we gonna dig deep into internals of maximum entropy policy.
MaxEnt Policy
For simplicity the authors discuss this part for the MDP case. A policy $\pi$, through its interaction with an MDP, induces a t-step state distribution over the state space $S$,
$$ d _ {t,\pi} (s) = p(s_t=s | \pi) $$
The objective of maximum entropy exploration is given by:
$$ \mathcal{H}(d(.)) = -\mathbb{E} _ {s \sim d} \left[ \log{d(s)} \right] $$
Where $d$ can be regarded as either,
- Stationary state distribution (infinite horizon): $d _ {\pi} = \lim _ {t \rightarrow \infty} d _ {t,\pi} (s)$
- Discounted state distribution (infinite horizon): $d _ {\gamma, \pi} = (1-\gamma) \sum _ {t=0} ^ {\infty} \gamma^t d _ {t,\pi} (s)$
- Marginal state distribution (finite horizon): $d _ {T, \pi} = \frac{1}{T} \sum _ {t=0} ^ {T} d _ {t,\pi} (s)$
In this work they focus on the finite horizon setting and adapt the marginal state distribution $d _ {T, \pi}$ in which $T$ equals the episode horizon $H$, so we seek to maximize the objective:
$$ \begin{align*} \mathcal{R} _ {\mathcal{H}} (\pi) &= \mathbb{E} _ {M \sim \hat{P}(M)} \left[ \mathcal{H}(d _ {H,\pi}) \right] \\ &=\mathbb{E} _ {M \sim \hat{P}(M)} \left[ \mathcal{H}(\frac{1}{H} \sum _ {t=0} ^ {H} d _ {t,\pi} (s)) \right] \end{align*} $$
which yields a policy that “equally” visits all states during the episode.
To maximize this objective we can estimating the density of the agent’s state visitation distribution, but in this paper the authors adapt the non-parametric entropy estimation approach; we estimate the entropy using the particle based k-nearest neighbor (k-NN estimator).
To estimate the distribution $d _ {H,\pi}$ over the states $S$, we consider each trajectory as $H$ samples of states $\{ s_t \} _ {t=1} ^ {H}$ and take $s _ t ^ {\text{k-NN}}$ to be the k-NN of the state $s_t$ within the trajectory,
$$ \hat{ \mathcal{H} } ^ {k,H} (d _ {H,\pi}) \approx \frac{1}{H} \sum _ {t=1} ^ {H} \log ( \parallel s_t - s_t^{\text{k-NN}} \parallel _ 2) $$
In which we define intrinsic reward function as,
$$ r_I (s_t) \coloneqq \log ( \parallel s_t - s_t^{\text{k-NN}} \parallel _ 2) $$
This formulation enables us to deploy any RL algorithm to approximately optimize objective.
Specifically, in this work we use the policy gradient algorithm PPOو where at every time step $t$, the state $s_t^{\text{k-NN}}$ is chosen from previous states $\{ s_t \} _ {t=1} ^ {t-1}$ of the same episode. To improve computational efficiency, instead of taking the full observation as the state (64 x 64 RGB image), we sub-sample the observation by applying average pooling of 3 x 3 to produce an image of size 21 x 21.
We found that agents trained for maximum entropy exploration exhibit a smaller generalization gap compared with the standard approach of training solely with extrinsic reward. The policies are equipped with a memory unit (GRU) to allow learning of deterministic policies that maximize the entropy.
In all three environments, we demonstrate a small generalization gap, as test performance on unseen levels closely follows the performance achieved during training.

In addition, we verify that the train results are near optimal by comparing with a hand designed approximately optimal exploration policy. For example, on Maze we use the well known maze exploring strategy wall follower, also known as the left/right-hand rule.
ExpGen Algorithm
Our main insight is that, given the generalization property of the entropy maximization policy established above, an agent can apply this behavior in a test MDP and expect effective exploration at test time. We pair this insight with the epistemic POMDP idea, and propose to play the exploration policy when the agent faces epistemic uncertainty, hopefully driving the agent to a different state where the reward-seeking policy is more certain.
Our framework comprises two parts: an entropy maximizing network and an ensemble of networks that maximize an extrinsic reward to evaluate epistemic uncertainty. The first step entails training a network equipped with a memory unit to obtain a maxEnt policy $\pi_H$ that maximizes entropy. Next, we train an ensemble of memory-less policy networks $\{ \pi _ r ^ j \} _ {j=1} ^ {m} $ to maximize extrinsic reward.
Here is the ExpGen algorithm,

We consider domains with a finite action space, and say that the policy $\pi _ r ^ i$ is certain at state $s$ if its action $a_i \sim \pi _ r ^ i (a|s)$ is in consensus with the ensemble: $a_i = a_j$ for the majority of $k$ out of $m$, where $k$ is a hyperparameter of our algorithm.

Switching between two policies may result in a case where the agent repeatedly toggles between two states (if, say, the maxEnt policy takes the agent from state $s_1$ to a state $s_2$, where the ensemble agrees on an action that again moves to state $s_1$.). To avoid such “meta-stable” behavior, we randomly choose the number of maxEnt steps $n_{\pi_{\mathcal{H}}}$ from a Geometric distribution, $n_{\pi_{\mathcal{H}}} \sim Geom(\alpha)$.
Experiments
Our experimental setup follows ProcGen’s easy configuration, wherein agents are trained on 200 levels for 25M steps and subsequently tested on random levels. All agents are implemented using the IMPALA (Importance Weighted Actor-Learner Architectures) convolutional architecture, and trained using PPO or IDAAC. For the maximum entropy agent $\pi_H$ we incorporate a single GRU at the final embedding of the IMPALA convolutional architecture. For all games, we use the same parameter $\alpha=0.5$ of the Geometric distribution and form an ensemble of 10 networks.

Following figure is comparison across all ProcGen games, with 95% bootstrap CIs highlighted in color. Score distributions of ExpGen, PPO, PLR, UCB-DrAC, PPG and IDAAC.

Following figure shows in each row, the probability of algorithm X outperforming algorithm Y. The comparison illustrates the superiority of ExpGen over the leading contender IDAAC with probability 0.6, as well as over other methods with even higher probability.

See Also
- PyTorch implementation of ExpGen @ GitHub
- Ev Zisselman Presentation @ NeurIPS 2023
- ExpGen Rebuttal Process @ OpenReview
- ExpGen Poster for NeurIPS 2023